Probabilistic Graphical Model

blairchen

Publish：Jun 8, 2019

对于一个实际问题，目标：能够挖掘隐含在数据中的知识。怎样才能使用概率图模型挖掘这些隐藏知识呢？

用观测结点表示观测到的数据，用隐含结点表示潜在的知识，用边来描述知识与数据的相互关系，获一概率分布。

1. Probabilistic Graphical Model

概率图中的**节点**分为：

概率图中的**边** 分为：

常见的概率图模型： Native Bayes、最大熵、隐马尔科夫模型、CRF、LDA 等.

PGM 联合概率:

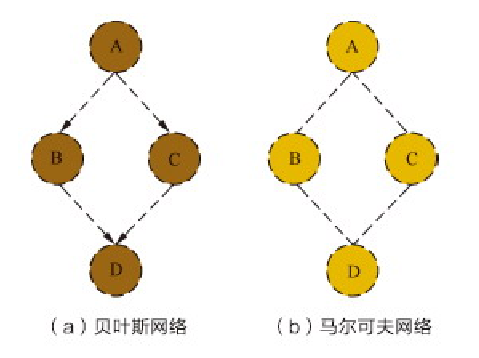
概率图模型最为“精彩”的部分就是能够用简洁清晰的图示形式表达概率生成的关系:

在给定A的条件下B和C是条件独立的，基于条件概率的定义可得：

\begin{aligned} P(C | A, B) &=\frac{P(B, C | A)}{P(B A)}=\frac{P(B | A) P(C | A)}{P(B | A)} \\\\ &=P(C | A) \end{aligned}

同理，在给定B和C的条件下A和D是条件独立的，可得：

\begin{aligned} P(D | A, B, C) &= \frac{P(A, D | B, C)}{P(A | B, C)}=\frac{P(A | B, C) P(D | B, C)}{P(A | B, C)} \\\\ &= P(D | B, C) \end{aligned}

结合上面的两个表达式可得联合概率：

\begin{aligned} P(A,B,C,D)&=P(A)P(B|A)P(C|A,B)P(D|A,B,C) \\\\ &= P(A)P(B|A)P(C|A)P(D|B,C) \end{aligned}\tag{6.3}

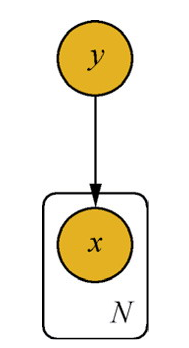
解释朴素贝叶斯模型的原理，并给出概率图模型表示:

通过预测指定样本属于特定类别的概率

y=\max \_{y\_{i}} P\left(y\_{i} | x\right)

可以写成：

P\left(y\_{i} | x\right)=\frac{P\left(x | y\_{i}\right) P\left(y\_{i}\right)}{P(x)}

其中 $x=\left(x\_{1}, x\_{2}, \ldots \ldots, x\_{n}\right)$ , 为样本对应的特征向量， $P(x)$ 为样本的先验概率。

generative approach 由数据学习到联合概率分布 $P(X,Y)$ ，然后求出条件概率分布 $P(Y\mid X)$ 作为预测的模型：

P(Y\mid X)=\frac{P(X,Y)}{P(X)}

典型的生成式模型包括： Native Bayes、HMM、Bayes Net

discriminative approach 由数据直接学到决策函数 $f(X)$ 或条件概率分布 $P(Y\mid X)$ 作为预测的模型：

f(X), P(Y\mid X)

判别式模型关心的是对于给定的输入 $X$ , 应该预测什么样的输出 $Y$ , 判别模型就是判别数据输出量的模型。

典型的判别式模型包括： LR、NN、SVM、CRF、CART

vs	generative approach	discriminative approach
定义	由数据学习联合概率分布 $P(X,Y)$ 然后, 求出在 $X$ 情况下， $P(Y)$ 作为预测的模型	决策函数 $f(x)$ 或条件概率分布 $P(X)$ 作为预测模型
特点	1. 可还原出 $P(X,Y)$ ； 2. 学习收敛速度更快； 3. 存在隐变量时仍可用	1. 直接面对预测，准确率更高些; 2. 便于数据抽象，特征定义使用;
模型	native bayes、hidden markov	Logistic Regression、SVM、Gradient Boosting、CRF…
Note	给定输入 $X$ 产生输出 $Y$ 的生成关系	对给定的输入 $X$ ，应预测什么样的输出 $Y$