Logistic Regression

blairchen

data-science

Publish：May 31, 2019

views

Logistic Regression 是一种用于解决二分类（0 or 1）问题的机器学习方法.

举个🌰 :

(1). 用户购买某商品的可能性

(2). 某病人患有某种疾病的可能性

(3). 某广告被用户点击的可能性等

1. Logistic vs Linear Regression

Logistic Regression 和 Linear Regression 都是一种广义线性模型（generalized linear model）。

逻辑回归假设因变量 y 服从伯努利分布，而线性回归假设因变量 y 服从高斯分布。 因此与线性回归有很多相同之处，去除 Sigmoid 映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过 Sigmoid函数 引入了非线性因素，因此可以轻松处理 0/1 分类问题。

1.1 Linear Regression

$z={\theta\_{0}}+{\theta\_{1}x\_{1}}+{\theta\_{2}x\_{2}+{\theta\_{3}x\_{3}}...+{\theta\_{n}x\_{n}}}=\theta^Tx$

使用最小二乘法求解 Linear Regression 时，我们认为因变量 y 服从正态分布。

线性回归假设因变量 y 服从高斯分布: 真实值y与拟合值Y之间的差值是不是符合正态分布。

1.2 Logistic Regression

$h\_{\theta}(x)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta^Tx}}$

Logistic Regression 将线性函数的结果映射到了 sigmoid 函数 中. 取值在 [0

$log\frac{p}{1-p} = \theta^Tx$

一件事发生的几率 $odds = \frac{p}{1-p}$， $p = P(y=1|x)$

Logistic Regression 可以看作是对于 “y=1|x” 这一事件的对数几率的线性回归.

逻辑回归通过对似然函数 $
L(\theta)=\prod_{i=1}^{{N}P(y_i|x_i;\theta)=\prod_{i=1}}{N}(\pi(x_i))^{{y_i}(1-\pi(x_i))}{1-y_i} $ 的学习，得到最佳参数 θ.

Logistic 与 Linear Regression 二者都使用了极大似然估计来对训练样本进行建模

迭代自己 Logistic Regression

2. LR Hypothesis function

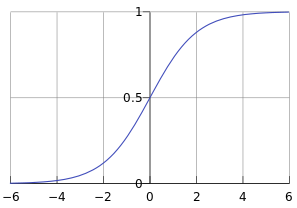
其函数曲线如下：

取值在[0

Logistic Regression 假设函数形式如下：

所以：

一个机器学习的模型，实际上是把决策函数限定在某一组条件下，这组限定条件就决定了模型的假设空间。当然，我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是：

这个函数的意思就是在给定 x 和 0 的条件下 y=1 的概率

3. Cost Function

Cost Function：

Loss Function：

上面的方程等价于：

• 选择 Cost_Function 时，最好挑选对参数 $\theta$ 可微的函数（全微分存在，偏导数一定存在）
• 对于每种算法来说，Cost_Function 不是唯一的； Cost_Function 是参数 $\theta$ 的函数；
• Cost Function 是对所有样本而言, Loss Function 是对单一样本而言.
• $J(\theta)$ 是一个标量, 我们需要 min 最小化它.

LR 中，代价函数是交叉熵 (Cross Entropy)，交叉熵是一个常见的代价函数:

good 简单的交叉熵损失函数，你真的懂了吗？

4. Cross Entropy

Cross Entropy 是信息论中的一个概念，要想了解交叉熵的本质，需要先从最基本的概念讲起。

信息量、熵、相对熵（KL散度）、交叉熵

同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)， 用 KL散度 来衡量这两个分布的差异。

D\_{KL}(p||q)=\sum\_{i=1}^np(x\_i)log(\frac{p(x\_i)}{q(x\_i)}) \tag{3.1}

\begin{eqnarray} D\_{KL}(p||q) &=& \sum\_{i=1}^np(x\_i)log(p(x\_i))-\sum\_{i=1}^np(x\_i)log(q(x\_i))\end{eqnarray}

等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

\begin{eqnarray} =& -H(p(x))+[-\sum\_{i=1}^np(x\_i)log(q(x\_i))] \end{eqnarray}

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即 $D\_{KL}(y||\hat{y})$ .

由于KL散度中的前一部分 $-H(y)$ 不变，故在优化过程中，只需要关注 Cross Entropy 就可以了。

所以一般在机器学习中直接用用 Cross Entropy Loss，评估模型。

$D\_{KL}$ 的值越小，表示 q分布 和 p分布 越接近.

一文搞懂交叉熵在机器学习中的使用

交叉熵在多分类问题中的使用, sigmoid

1）CrossEntropy lossFunction

二分类:

意义：能表征 真实样本标签 和 预测概率 之间的差值

2）最小化交叉熵的本质就是对数似然函数的最大化；

3）对数似然函数的本质就是衡量在某个参数下，整体的估计和真实情况一样的概率，越大代表越相近；

4）损失函数的本质就是衡量预测值和真实值之间的差距，越大代表越不相近。

4.1 Log 设计理念

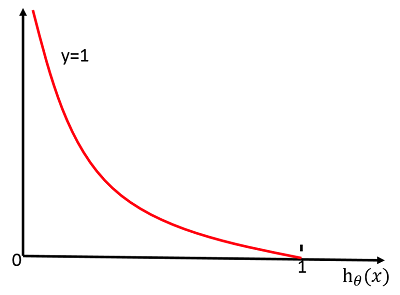
预测输出与 y 差得越多，L 的值越大，也就是说对当前模型的 “ 惩罚 ” 越大，而且是非线性增大，是一种类似指数增长的级别。这是由 log 函数本身的特性所决定的。这样的好处是 模型会倾向于让预测输出更接近真实样本标签 y。

我们希望 log P(y|x) 越大越好，反过来，只要 log P(y|x) 的负值 -log P(y|x) 越小就行了。那我们就可以引入损失函数，且令 Loss = -log P(y|x)即可。则得到损失函数为：

图可以帮助我们对 CrossEntropy lossFunction 有更直观的理解。无论真实样本标签 y 是 0 还是 1，L 都表征了预测输出与 y 的差距。

4.2 MLE 最大似然

就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的 模型参数值！

输入有两个：$x$ 表示某一个具体的数据；$θ$ 表示模型的参数。

Probability Function：

对于这个函数： $P(x|θ)$ ， 如果 $θ$ 是已知确定的，$x$ 是变量，这个函数叫做概率函数 (probability function)，它描述对于不同的样本点 $x$，其出现概率是多少。

Likelihood Function：

如果 $x$ 是已知确定的，$θ$ 是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现 $x$ 这个样本点的概率是多少。

MLE 提供了一种 给定观察数据来评估模型参数 的方法，即：“模型已定，参数未知”。

MLE 中 采样 需满足一个重要的假设，就是所有的采样都是 独立同分布 的.

一句话总结：概率是已知模型和参数，推数据。统计是已知数据，推模型和参数。

5. 最小二乘法 vs 最大似然估计

总结一句话：

• 最小二乘法的核心是权衡，因为你要在很多条线中间选择，选择出距离所有的点之和最短的；
• 而极大似然的核心是自恋，要相信自己是天选之子，自己看到的，就是冥冥之中最接近真相的。^_

Reference

• 逻辑回归（Logistic Regression）（一）
• 广义线性模型（Generalized Linear Model）
• GLM(广义线性模型) 与 LR(逻辑回归) 详解
• 怎样用通俗易懂的文字解释正态分布及其意义？
• 最大似然估计和最小二乘法怎么理解？
• 知乎：一文搞懂极大似然估计
• CSDN：详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解
• 一文搞懂交叉熵在机器学习中的使用，透彻理解交叉熵背后的直觉

updated on：May 2, 2022

Logistic_Regression