User Credit Score

blairchen

data-science

Publish：Jun 23, 2019

views

Credit Score Card

信用评分卡模型是最常见的金融风控手段之一，它是指根据客户的各种属性和行为数据，利用一定的信用评分模型，对客户进行信用评分，据此决定是否给予授信以及授信的额度和利率，从而识别和减少在金融交易中存在的交易风险。

按照借贷用户的借贷时间，评分卡模型可以划分为以下三种：

• 贷前： Application score card， 又称为A卡
• 贷中： Behavior score card， 又称为B卡
• 贷后： Collection score card， 又称为C卡

申请评分卡要求最为严格，也最为重要，可解释性也要求最强，一般主流模型为 LR.

如需了解更多关于 互联网金融风控 的相关背景知识，请参阅：

• Internet Financial Risk Control (part1) ： The Fraud Risk of Financial Technology Enterprises

• Internet Financial Risk Control (part2) ： model strategy

• Internet Financial Risk Control (part3) ： Lending Club Data dev

1. 数据获取

• 金融机构自身字段： 年龄，户籍，性别，收入，…；
• 第三方机构的数据： 消费行为…

数据情况：

23W+ 去掉一些灰用户，剩余

M1标准： 好/坏: 13W+ 坏 4K

30~50 : 1 都是正常的

2. EDA

Exploratory Data Analysis

每个字段的缺失值情况、异常值情况、平均值、中位数、最大值、最小值、分布情况等

• 牛顿插值的几何解释是怎么样的？
• 如何直观地理解拉格朗日插值法？
• 从牛顿插值法到泰勒公式
• 泰勒公式一句话描述：就是用多项式函数去逼近光滑函数

缺失值的处理，还可以用 RF 去拟合.

3. 数据预处理

(1). 数据清洗

(2). 变量分箱

(3). WOE 编码

1. 缺失值太多
2. 非数值变量多 (emp_title…)
3. id, member_id 等
4. loan_amnt != df.funded_amnt
5. 空值填充为 0
6. 带 % 的浮点，去掉 %

好坏比是 34:1 是非常难以处理的样本了.

3.1 数据清洗

缺失值太多

1
2
3
4
5
6
7
8
9

# 处理对象类型的缺失，unique
df.select_dtypes(include=['O']).describe().T.\
assign(missing_pct=df.apply(lambda x : (len(x)-x.count())/float(len(x))))

# 缺失值特别高的可以删除掉

# 我们可以对 非数值型 变量，做一个循环，发现 zip_code 有 873 个 unique 的值，那么先不处理
for col in df.select_dtypes(include=['object']).columns:
    print ("Column {} has {} unique instances".format( col, len(df[col].unique())) )

3.2 变量分箱

• 对连续变量进行分段离散化；
• 将多状态的离散变量进行合并，减少离散变量的状态数。

先可以粗分箱，之后在合并。 比如 年龄取值数有 30个，那么分为 30 箱，最后合为 5 箱。
其他变量可能粗分箱为 100 箱，之后合并.

分箱方法很多，最常见的方法之一： Merge分箱中的 Chimerge 分箱.

Chimerge 其基本思想是如果两个相邻的区间具有类似的类分布，则这两个区间合并；
否则，它们应保持分开。Chimerge通常采用卡方值来衡量两相邻区间的类分布情况。

• 连续值按升序排列，离散值先转化为坏客户的比率，然后再按升序排列；
• 为了减少计算量，对于状态数大于某一阈值 (建议为100) 的变量，利用等频分箱进行粗分箱。
• 若有缺失值，则缺失值单独作为一个分箱。

分箱的最大区间数 & 分箱初始化

这里我取： n = 5

1. 连续值按升序排列，离散值先转化为坏客户的比率，然后再按升序排列；
2. 为了减少计算量，对于状态数大于某一阈值 (建议为100) 的变量，利用等频分箱进行粗分箱。
3. 若有缺失值，则缺失值单独作为一个分箱。

合并区间：

1. 将卡方值最小的一对区间合并

分箱后处理：

1. 对于坏客户比例为 0 或 1 的分箱进行合并 (一个分箱内不能全为好客户或者全为坏客户)。
2. 对于分箱后某一箱样本占比超过 95% 的箱子进行删除。
3. 检查缺失分箱的坏客户比例是否和非缺失分箱相等，如果相等，进行合并。

总结一下特征分箱的优势：

1. 特征分箱可以有效处理特征中的缺失值和异常值。
2. 特征分箱后，数据和模型会更稳定。
3. 特征分箱可以简化逻辑回归模型，降低模型过拟合的风险，提高模型的泛化能力。
4. 将所有特征统一变换为类别型变量。
5. 分箱后变量才可以使用标准的评分卡格式，即对不同的分段进行评分。

列表内容特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；

• 变量分箱实践
• One-Hot编码与哑变量
• 方差、标准差和均方根误差的区别总结
• 基于卡方分箱的评分卡建模

good 基于卡方分箱的评分卡建模 , 卡方分布—chi-square distribution, χ2-distribution

卡方值的意义,举个例子：

某医院对某种病症的患者使用了 $A$，$B$ 两种不同的疗法，结果如表1，问两种疗法有无差别？

可以计算出各格内的期望频数：

第1行1列： 43×53/87=26.2 ,

第1行2列： 43×34/87=16.8 ,

第2行1列： 44×53/87=26.8 ,

第2行2列： 44×34/87=17.2

A箱

(26.2-19)*(26.2-19) / 26.2 -> (26.2 是 正类的期望频数， 19 是真实频数)

(16.8-24)*(16.8-24) / 16.8 (16.8 是 负类的期望频数)

B箱

(26.8-34)*(26.8-34) / 26.8 (26.8 是 正类的期望频数)

(17.2-10)*(17.2-10) / 17.2 (17.2 是 负类的期望频数)

先建立原假设：A、B两种疗法没有区别。根据卡方值的计算公式，计算：卡方值=10.01。得到卡方值以后，接下来需要查询卡方分布表来判断p值，从而做出接受或拒绝原假设的决定。

点击时的区域标题： 卡方分布—chi-square distribution, χ2-distribution

χ2-distribution:

若 $k$ 个独立的随机变量 $Z\_1, Z\_2, ..., Z\_k$ 满足标准正态分布 $N(0,1)$ , 则这 $k$ 个随机变量的平方和：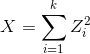

卡方检验—χ2检验是以χ2分布为基础的一种假设检验方法，主要用于分类变量之间的独立性检验

思想是根据样本数据推断 总体分布与期望分布 是否有显著性差异，或者推断两个分类变量是否相关或者独立。

一般可以设原假设为 ：观察频数与期望频数没有差异，或者两个变量相互独立不相关。

实际应用中，我们先假设原假设成立，计算出卡方值，卡方表示观察值与理论值间的偏离程度。

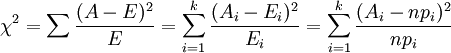
卡方值只是一个中间过程，通过卡方值计算出p值，p值才是我们最重要需要的。p小于0.05意味着存在显著差异。

卡方值是非参数检验中的一个统计量，主要用于非参数统计分析中。它的作用是检验数据的相关性。如果卡方值的显著性（即SIG.）小于0.05，说明两个变量是显著相关的。

3.3 WOE (weight of evidence)

WOE 称为证据权重(weight of evidence) , 将离散变量转化为连续变量。

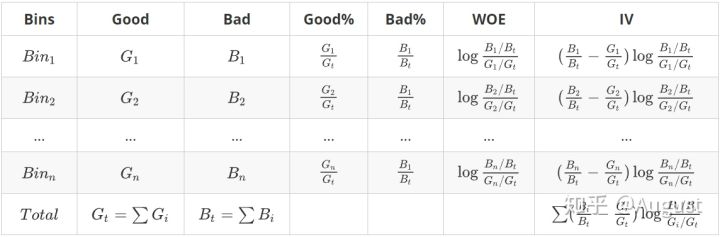
WOE 将预测类别的集中度的属性作为编码的数值。对于自变量第 $i$ 箱的WOE值为：

$p\_{i1}$ 是第 $i$ 箱中坏客户占所有坏客户比例

$p\_{i0}$ 是第 $i$ 箱中好客户占所有好客户比例

WOE: 当前分箱中坏客户和好客户的比值，和所有样本中这个比值的差异

当分箱中坏客户和好客户的比例等于随机坏客户和好客户的比值时，说明这个分箱没有预测能力，即WOE=0。 (WOE为0，说明该箱出的特征对结果没有区分度)

实际上WOE编码相当于把分箱后的特征从非线性可分映射到近似线性可分的空间内:

总结一下WOE编码的优势：

1. 可提升模型的预测效果
2. 将自变量规范到同一尺度上
3. WOE能反映自变量取值的贡献情况
4. 有利于对变量的每个分箱进行评分
5. 转化为连续变量之后，便于分析变量与变量之间的相关性
6. 与独热向量编码相比，可以保证变量的完整性，同时避免稀疏矩阵和维度灾难

4. 变量筛选

主要衡量标准: 变量的预测能力和变量的线性相关性。

挑选入模变量:

1. 变量的预测能力
2. 变量之间的线性相关性
3. 变量在业务上的可解释性

变量两两相关性分析，变量的多重共线性分析。

4.1 单变量筛选

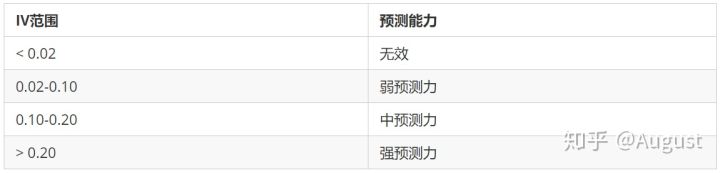
IV 信息价值(information value)，自变量的IV值越大，表示自变量的预测能力越强。 类似指标还有信息增益等。

变量对应的IV值为所有分箱对应的 IV 值之和：

IV 值实际上式变量各个分箱的加权求和。且和决策树中的交叉熵有异曲同工之妙。以下为交叉熵公式：

IV值的具体的计算流程如下：

IV排序后，选择IV>0.02的变量，共58个变量IV>0.02

4.2 多变量分析

保留相关性低于阈值0.6的变量，剩余27个变量

为什么要进行相关性分析？

理想状态下，系数权重会有无数种取法，使系数权重变得无法解释，导致变量的每个分段的得分也有无数种取法（后面我们会发现变量中不同分段的评分会用到变量的系数）

总结一下变量筛选的意义：

1. 剔除跟目标变量不太相关的特征
2. 消除由于线性相关的变量，避免特征冗余
3. 减轻后期验证、部署、监控的负担
4. 保证变量的可解释性

特征相关度筛选

1
2
3
4

cor = df.corr()
cor.loc[:,:] = np.tril(cor, k=-1) # below main lower triangle of an array
cor = cor.stack()
cor[(cor > 0.55) | (cor < -0.55)] # 特征相关度筛选

4.3 显著性分析

删除P值不显著的变量，剩余12个变量了。

GBDT, GBRT, Xgboost, RF grid search

1
2
3
4
5
6

param_grid = {
    'learning_rate': [0.1, 0.05, 0.02, 0.01],
    'max_depth': [1,2,3,4],
    'min_samples_split': [50,100,200,400],
    'n_estimators': [100,200,400,800]
}

特征重要度：

1
2
3
4

# Top Ten， GBRT top 10 的参数有哪些，可以作为参考， GBRT 不仅是一个分类器，还能帮你筛选变量
# 比如 feature_importance = 0 的话，那么下一次 这个特征，你就去掉就可以了
# 重新用模型GBRT重新跑，或者用其他模型LR跑
# 或者其他的 RF 也可以帮助你做特征筛选

最后选择出 84 个变量， 然后在放到不同的模型中做训练，在 ensemble 应该效果还是不错的。

特征不稳定的，不可以作为入模变量：

挑选变量的时候，开始每个月我一直在看它的均值和方差的变化是否在容忍的范围内，超过50%舍

5. 转化为评分卡

将 odds 带入可得：

评分卡的分值可以定义为比率对数的线性表达来，即：

最终得到评分卡模型：

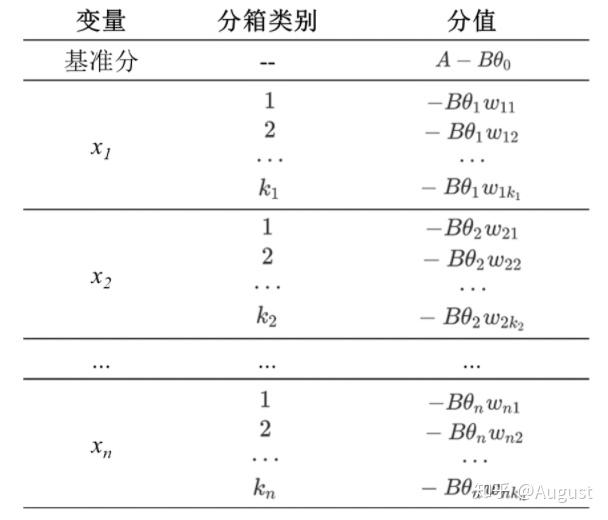
需要设定两个假设：

• 某个特定的违约概率下的预期评分，即比率 即比率 $\text{odds}$ 为 $θ\_0$ 时的分数为 $P\_0$
• 该odds为$2θ\_0$情况下评分的减少量（PDO）

6. KS 评估

K-S曲线其实数据来源和本质和ROC曲线是一致的，只是ROC曲线是把真正率和假正率当作横纵轴，而K-S曲线是把真正率和假正率都当作是纵轴，横轴则由选定的阈值来充当。

由于ks值能找出模型中差异最大的一个分段，因此适合用于cut_off，像评分卡这种就很适合用ks值来评估。但是ks值只能反映出哪个分段是区分最大的，而不能总体反映出所有分段的效果，因果AUC值更能胜任。

KS值表示了模型将+和-区分开来的能力。值越大，模型的预测准确性越好。

KS 值表示了模型区分好坏客户的能力。

等分 10 份，两条洛伦兹曲线， TPR 与 FPR 的差值. 好坏客户的区程度.

其实质是 $TPR - FPR$ 随好坏客户阈值变化的最大值。KS 值越大，模型的预测准确性越好。一般，KS > 0.4 即认为模型有很好的预测性能。

Reference

• Python三大评分卡之行为评分卡
• 玩转逻辑回归之金融评分卡模型
• 拍拍贷教你如何用GBDT做评分卡
• 模型区分度指标 KS 值
• 分类模型评判指标 ROC，AUC，GINI，KS
• 深入理解KS
• AUC和KS指标
• 一文完全理解模型ks指标含义并画出ks曲线

updated on：Jun 28, 2021

Credit-Score