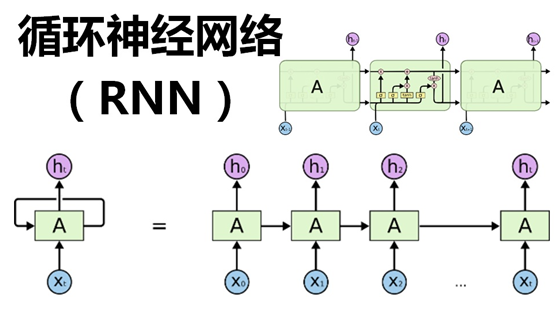
- 作为生物体,我们的视觉和听觉不断地获得带有序列的声音和图像信号,并交由大脑理解;
- 互联网数据中,很多是以序列形式存在的,例如文本、语音、视频、点击流等等。
RNN 基础知识,详参本博: Sequence Models
1. RNN Basic
在介绍 RNN 之前,首先解释一下为什么之前的标准网络不再适用了。因为它有两个缺点:
输入和输出的长度不尽相同无法共享从其他位置学来的特征
传统方法文本分类: 用一篇文章的 TF-IDF 向量作为输入,其中 TF-IDF 向量是词汇表大小.
Typical RNN Structure:
在 后面直接接一个 Softmax 层,输出文本所属类别的预测概率 ,就可以实现文本分类.
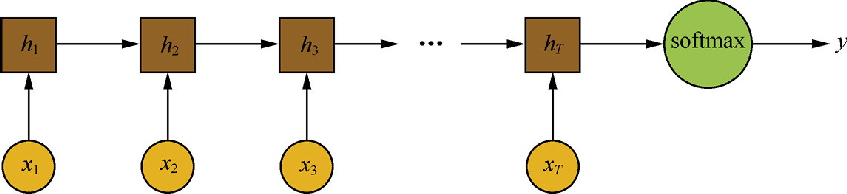
可应用于多种具体任务:
其中 和 为激活函数, 为输入层到隐含层的权重矩阵, 为隐含层从上一时刻到下一时刻状态转移的权重矩阵。在文本分类任务中, 可以选取 Tanh 函数或者 ReLU 函数, 可以采用 Softmax 函数。
1.1 TensorFlow RNN
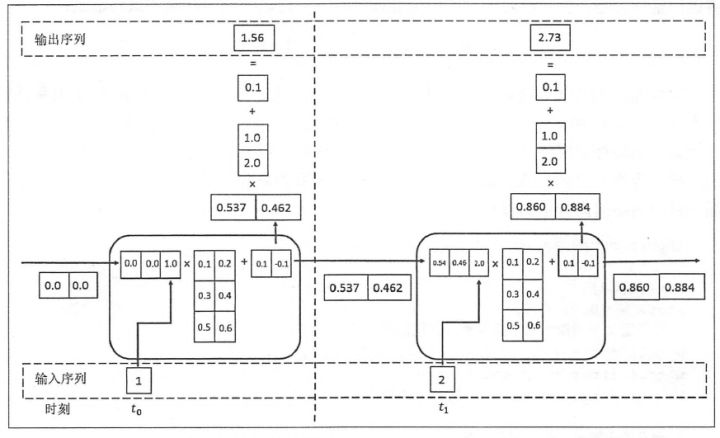
1.2 Forward Propagation
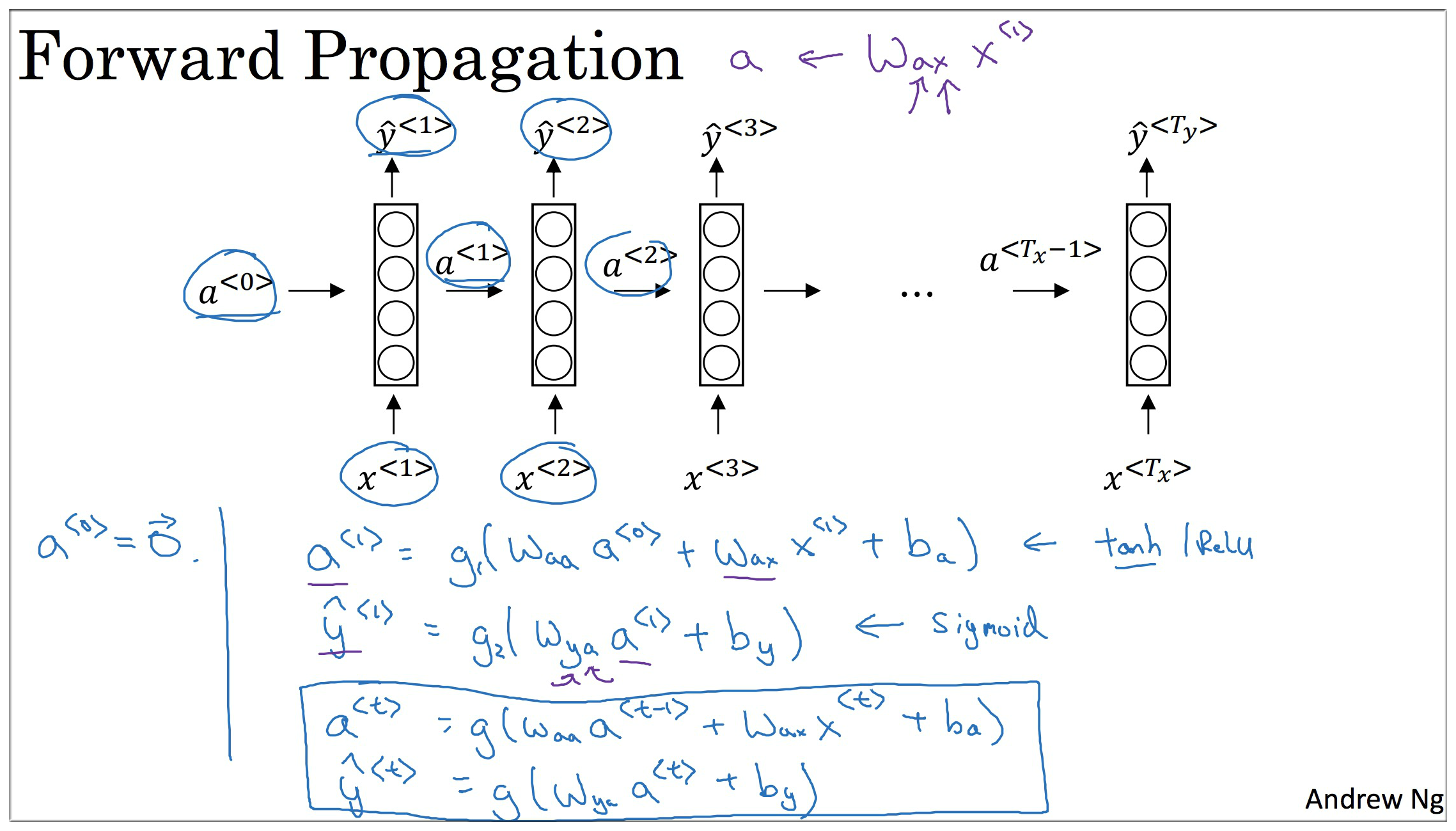
激活函数: 一般为
tanh函数 (orRelu函数), 一般是Sigmodorsoftmax函数.
1.3 RNN vs CNN
- RNN 优点: 最大程度捕捉上下文信息,这可能有利于捕获长文本的语义。
- RNN 缺点: 是一个有偏倚的模型,在这个模型中,后面的单词比先前的单词更具优势。因此,当它被用于捕获整个文档的语义时,它可能会降低效率,因为关键组件可能出现在文档中的任何地方,而不是最后。
- CNN 优点: 提取数据中的局部位置的特征,然后再拼接池化层。 CNN可以更好地捕捉文本的语义。是O(n)
- CNN 优点: 一个可以自动判断哪些特性在文本分类中扮演关键角色的池化层,以捕获文本中的关键组件。
2. Language model
此时就需要通过语言模型来预测每句话的概率:

2.1 RNN Language Model
- 首先我们需要一个很大的语料库 (Corpus)
- 将每个单词字符化 (Tokenize,即使用One-shot编码) 得到词典,,假设有 10000 个单词
- 还需要添加两个特殊的单词
- end of sentence. 终止符,表示句子结束.
- UNknown, 之前的笔记已介绍过
2.2 Language Model Example
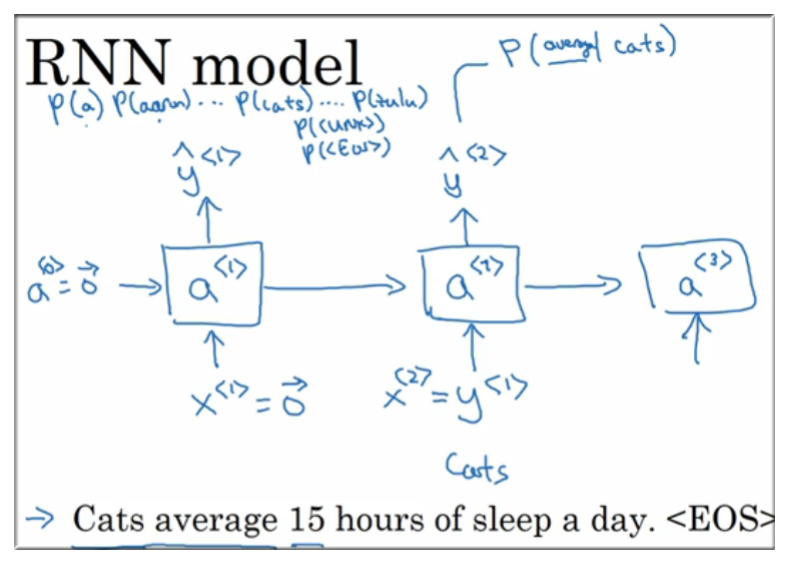
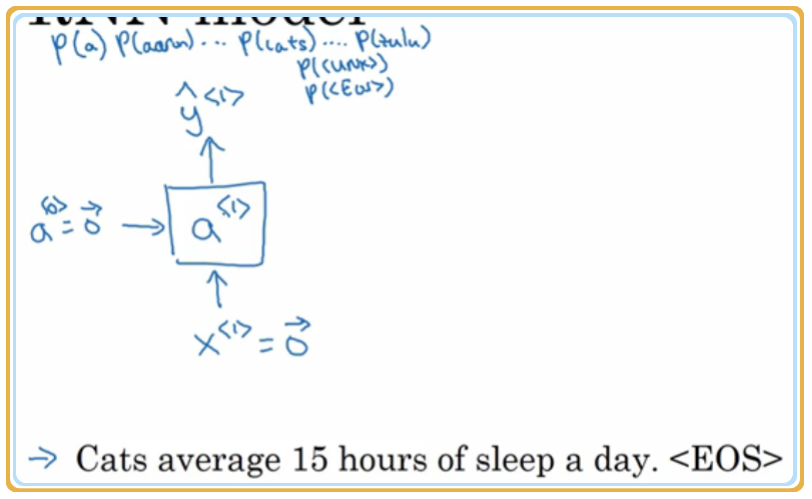
假设要对这句话进行建模:Cats average 15 hours of sleep a day.
1. 初始化
这一步比较特殊,即 和 都需要初始化为 .
此时 将会对第一个字可能出现的每一个可能进行概率的判断,即 .当然在最开始的时候没有任何的依据,可能得到的是完全不相干的字,因为只是根据初始的值和激活函数做出的取样。
2. 将真实值作为输入值:
之所以将真实值作为输入值很好理解,如果我们一直传错误的值,将永远也无法得到字与字之间的关系
如下图示,将 所表示的真实值 Cats 作为输入,即 得到
此时的
同理有
另外输入值满足:
3. 计算出损失值:
下图给出了构建模型的过程以及损失值计算公式:
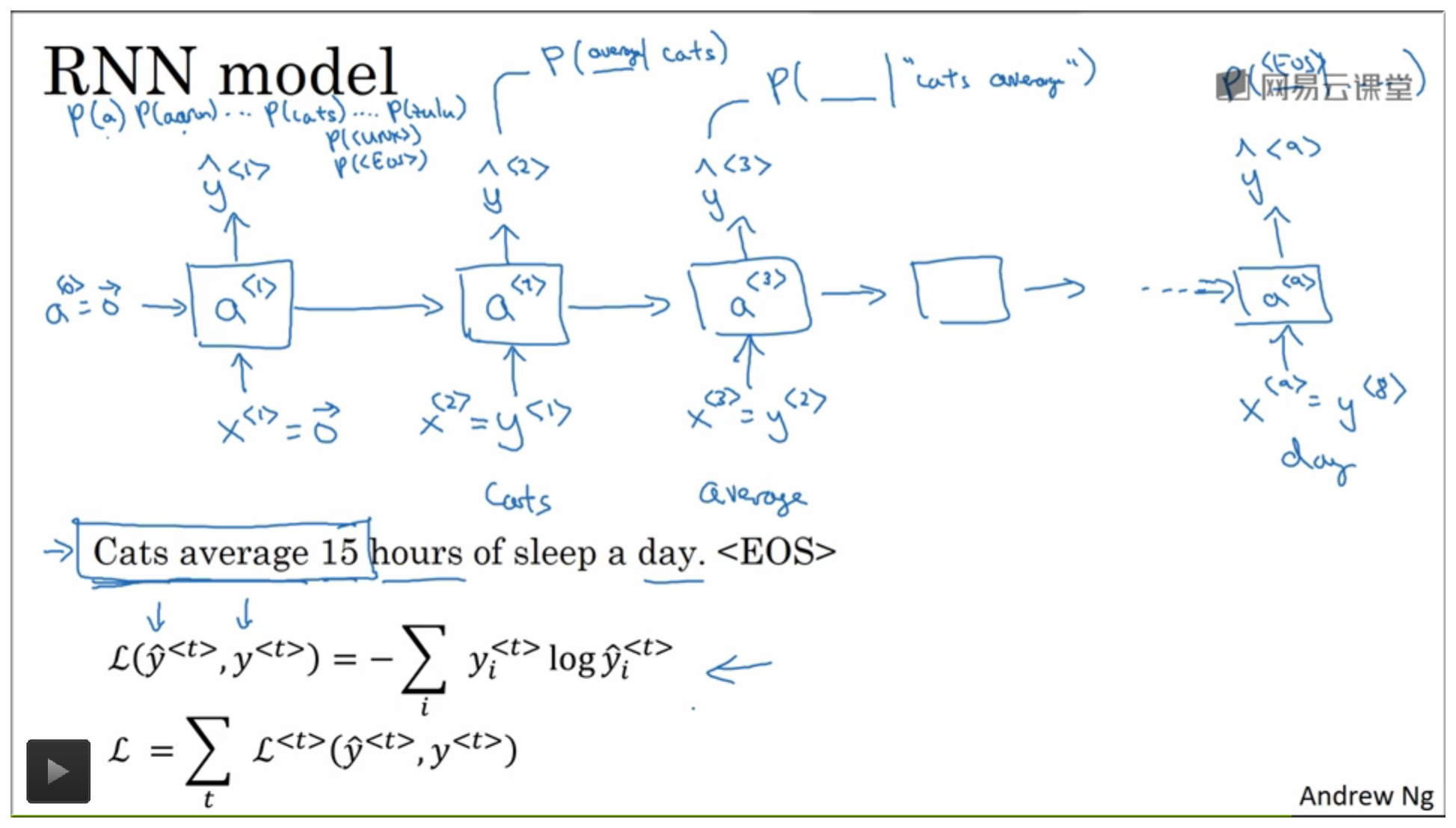
随着训练的次数的增多,或者常用词出现的频率的增多,语言模型便慢慢的会开始掌握简单的词语比如“平均”,“每天”,“小时”。一个完善的语言模型看到类似“ 10 个小”的时候,应该就能准确的判定下一个字是“时”。
(当然也许实际情况是“ 10 个小朋友”,所以通常会有更多的判断因素,这里只是一个例子)
3. Vanishing gradients with RNNs
目前这种基本的 RNN 也不擅长捕获这种长期依赖效应.
梯度爆炸可以用梯度消减解决、梯度消失就有点麻烦了,需要用 GRU 来解决.
gradient value 在 RNN 中也可能因为反向传播的层次太多导致 过小 或 过大
- 当梯度值过小的时候,网络无法有效调整自己权重矩阵致训练效果不佳,称为 gradient vanishing;
- 过大时直接影响到程序的运作因为程序已无法存储那么大的值,会返回 NaN ,称为 gradient exploding.
当 gradient 过大时, 可以每次将返回的梯度值进行检查,超出预定范围,则手动设为范围的边界值:
1 | if (gradient > max) { |
但梯度值过小的解决方案要稍微复杂一点,比如下面两句话:
“The cat,which already ate apple,yogurt,banana,…, was full.”
“The cats,which already ate apple,yogurt,banana,…, were full.”重点标出的 cat(s) 和 be 动词(was, were) 是有重要关联的,但是中间隔了一个 which 引导的定语从句,对于前面所介绍的基础的 RNN网络 很难学习到这个信息,尤其是当出现梯度消失时,而且这种情况很容易发生.
神经网络层次很多时,反向传播很难影响前面层次的参数。解决 gradient vanishing,提出了 GRU 单元.
将在接下来的两个章节介绍两种方法来解决 梯度过小 问题,目标是当一些重要的单词离得很远的时候,比如例子中的 “cat” 和 “was”,能让语言模型准确的输出单数人称过去时的 “was”,而不是 “is” 或者 “were”. 两个方法都将引入“记忆”的概念,也就是为 RNN 赋予一个记忆的功能.
4. GRU - Gated Recurrent Unit
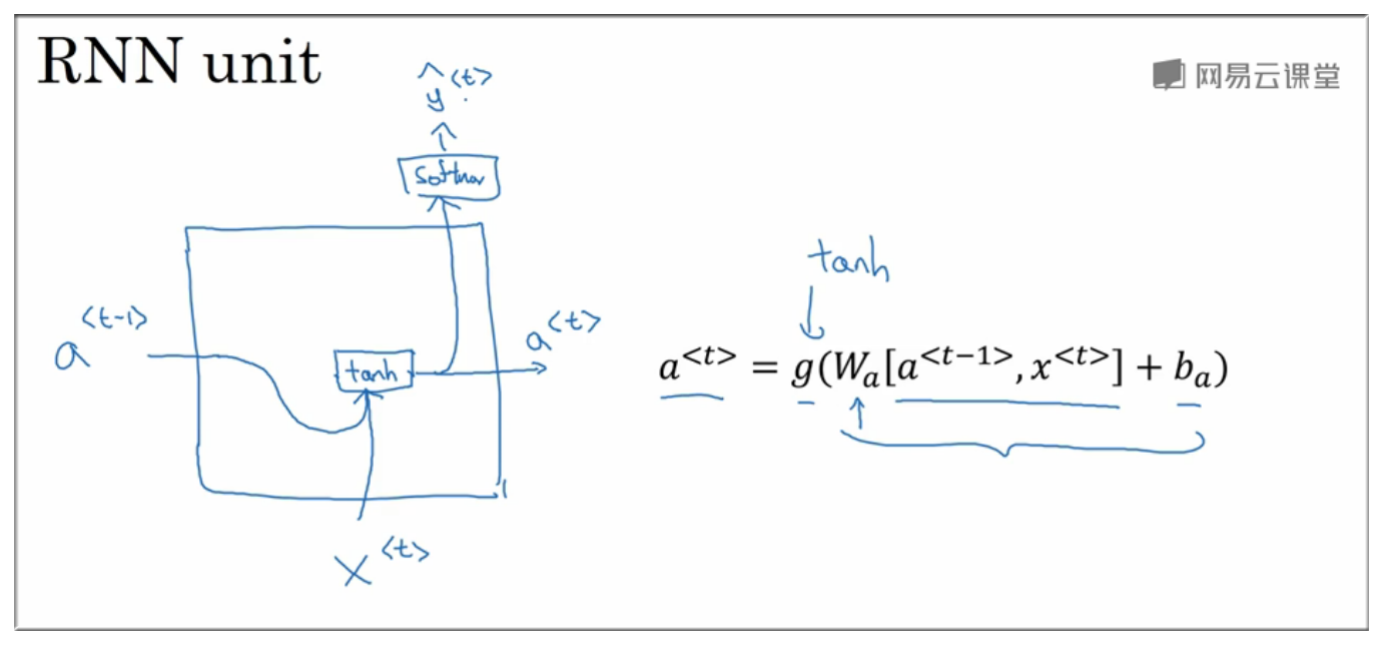
GRU 是一种用来解决梯度值过小的方法,首先来看下在一个时刻下的 RNN单元,激活函数为 tanh
4.1 回顾 RNN
输入数据为 和 , 与参数 进行线性运算后再使用 函数 转化得到 .
当然 , 再使用 softmax 函数处理可以得到预测值.
4.2 GRU结构
在 GRU中 会用到 “记忆细胞(Memory cell)” 这个概念, 我们用变量C表示。这个记忆细胞提供了记忆功能,例如它能够帮助记住 cat 对应 was, cats 对应 were.
而在 时刻,记忆细胞所包含的值其实就是 Activation function 值,即
注意:在这里两个变量的值虽然一样,但是含义不同。
另外在下节将介绍的 LSTM 中,二者值的大小有可能是不一样的,所以有必要使用这两种变量进行区分.
为了更新 memory_cell 的值,我们引入 来作为候选值从而来更新 ,其公式为:
更新门 (update gate):
更新门是 GRU 的核心概念,它的作用是用于判断是否需要进行更新.
更新门用 表示,其公式为:
如上图示, 值的大小大多分布在 0 或者 1,所以可以将其值的大小粗略的视为 0 或者 1。
这就是为什么我们就可以将其理解为一扇门,如果 , 就表示此时需要更新值,反之不用.
时刻记忆细胞:
有了更新门公式后,我们则可以给出 时刻 memory_cell 的值的计算公式:
c^{<{t}>} = \Gamma\_u \* \tilde{c} + (1-\Gamma\_u) \* c^{<{t-1}>}
公式很好理解,如果 ,那么 时刻 记忆细胞的值就等于候选值 , 反之等于前一时刻记忆细胞的值.
注:上面公式中的 * 表示元素之间进行乘法运算,而其他公式是 矩阵运算.
下图给出了该公式很直观的解释:
在读到 “cat” 时候,其他时候一直为 0,知道要输出 “was” 的时刻,我们知道 “cat” 的存在,也就知道它为单数
GRU 结构示意图
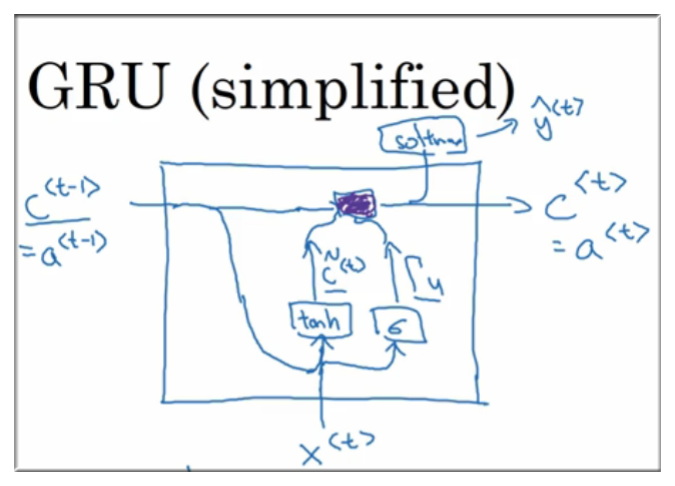
4.3 完整版 GRU
上面简化了 GRU,在完整版中还存在另一个符号 ,这符号的意义是控制 和 之间的联系强弱,完整版如下:
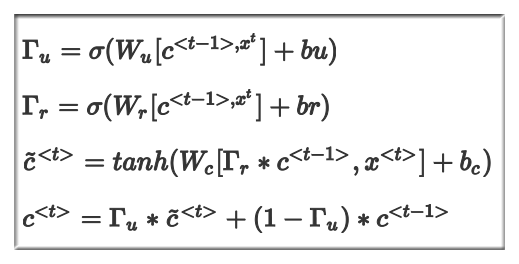
注意,完整公式中多出了一个 , 这个符号的作用是控制 和 之间联系的强弱.
5. LSTM - Long Short Term
介绍完 GRU 后,再介绍 LSTM 会更加容易理解。
5.1 GRU and LSTM
GRU 只有两个门,而 LSTM 有三个门,分别是更新门 (是否需要更新为 ),遗忘门 (是否需要丢弃上一个时刻的值),输出门 (是否需要输出本时刻的值)


下图是 LSTM 的结构示意图:
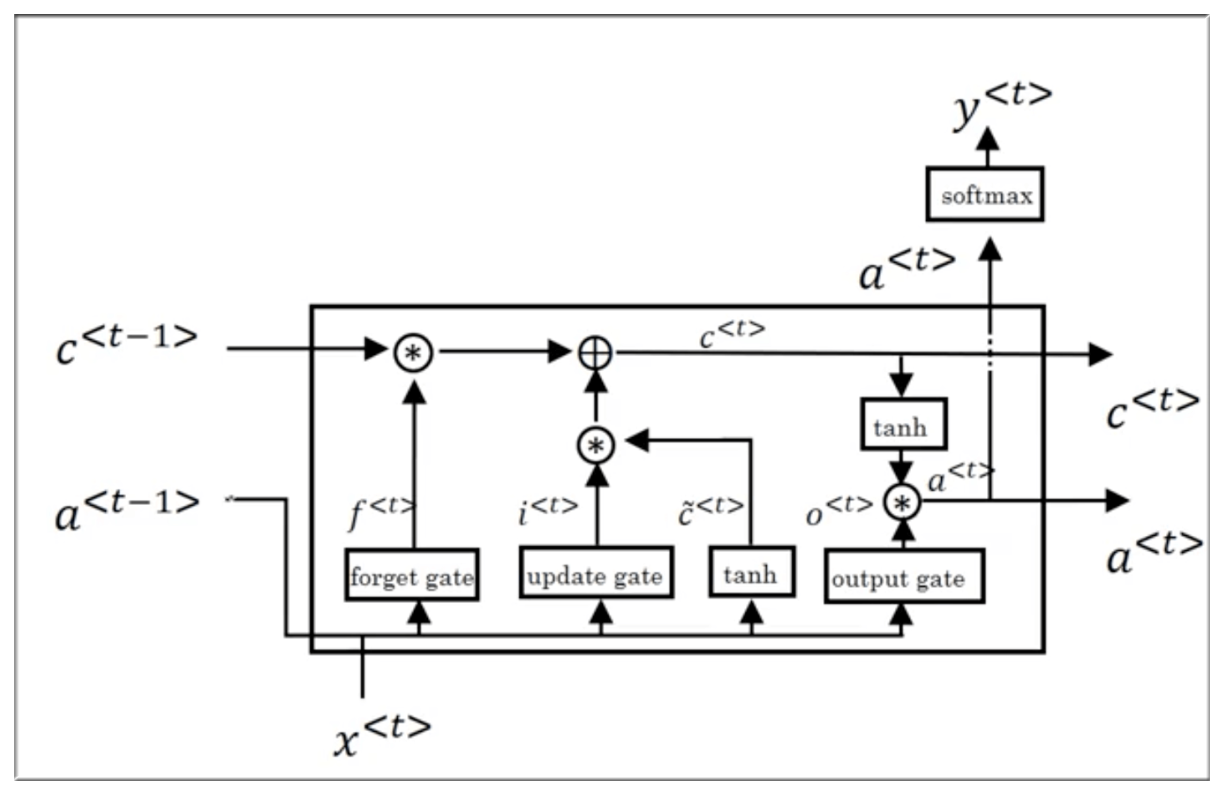
5.2 LSTM Structure
LSTM 仍是 和 来计算 ,但对内部的结构进行了更加精心的设计,加入 3 Gate 和 1 memory_cell.
输入门 : 控制 当前计算的新状态 以多大程度更新到记忆单元中 (也叫更新门);
遗忘门 : 控制 前一步记忆单元 中的信息有多大程度被遗忘掉;
输出门 : 控制当前的输出有多大程度上取决于 当前的记忆单元;
记忆单元 memory cell .
5.3 Activation function
在 LSTM 中, 关于 activation function 的选取:
- 、 和 使用 Sigmoid 函数作为激活函数;
- 在生成候选记忆时,使用 Tanh 作为激活函数。
注: 这两个激活函数都是饱和的,也就是说在输入达到一定值的情况下,输出就不会发生明显变化了。如果是用非饱和的激活函数,例如 ReLU,那么将难以实现门控的效果。
使用这个激活函数的原因如下:
(1). Sigmoid 输出在 0~1 之间。且当输入较大或较小时,其输出会非常接近1或0,从而保证该门开或关。
(2). 在生成候选记忆时,使用 Tanh 函数,是因为其输出在 −1~1 之间,这与大多数场景下特征分布是 0 中心的吻合。此外,Tanh 函数在输入为 0 附近相比 Sigmoid 函数有更大的梯度,通常使模型收敛更快。
总而言之,LSTM 经历了 20 年的发展,其核心思想一脉相承,但各个组件都发生了很多演化。
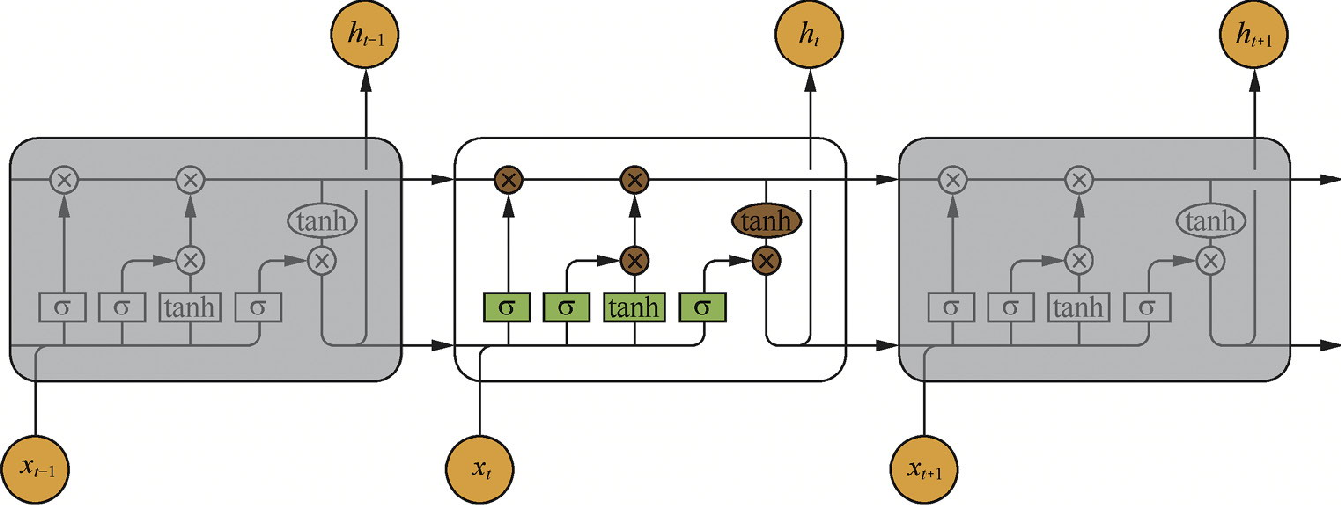
GRU vs LSTM
- GRU 和 LSTM 的效果在很多任务上不分伯仲。
- GRU 参数更少因此更容易收敛,但是数据集很大的情况下,LSTM表达效果更好,但计算量更大。
从结构上来说:
- GRU 只有两个门(update和reset),LSTM 有三个门(forget,input,output)
- GRU 直接将 hidden state 传给下一个单元,而 LSTM 则用 memory cell 把hidden state 包装起来。
6. Bidirectional RNN
前面介绍的都是单向的 RNN 结构,在处理某些问题上得到的效果不尽人意
如下面两句话,我们要从中标出人名:
Hesaid, “Teddy Roosevelt was a great President”.
Hesaid, “Teddy bears are on sale”.
- 第一句中的 Teddy Roosevelt 是人名
- 第二句中的 Teddy bears 是泰迪熊,同样都是单词 Teddy 对应的输出在第一句中应该是 1,第二句中应该是 0
像这样的例子如果想让我们的序列模型明白就需要借助不同的结构比如 - 双向递归神经网络(Bidirectional RNN).
该神经网络首先从正面理解一遍这句话,再从反方向理解一遍.
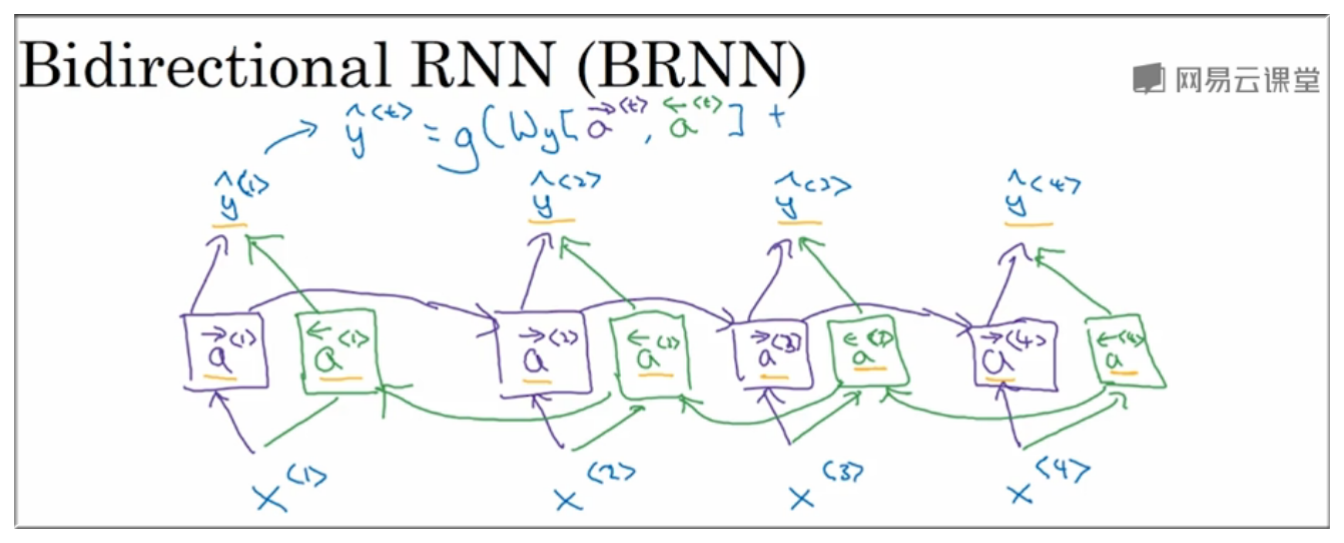
下图摘自大数据文摘整理
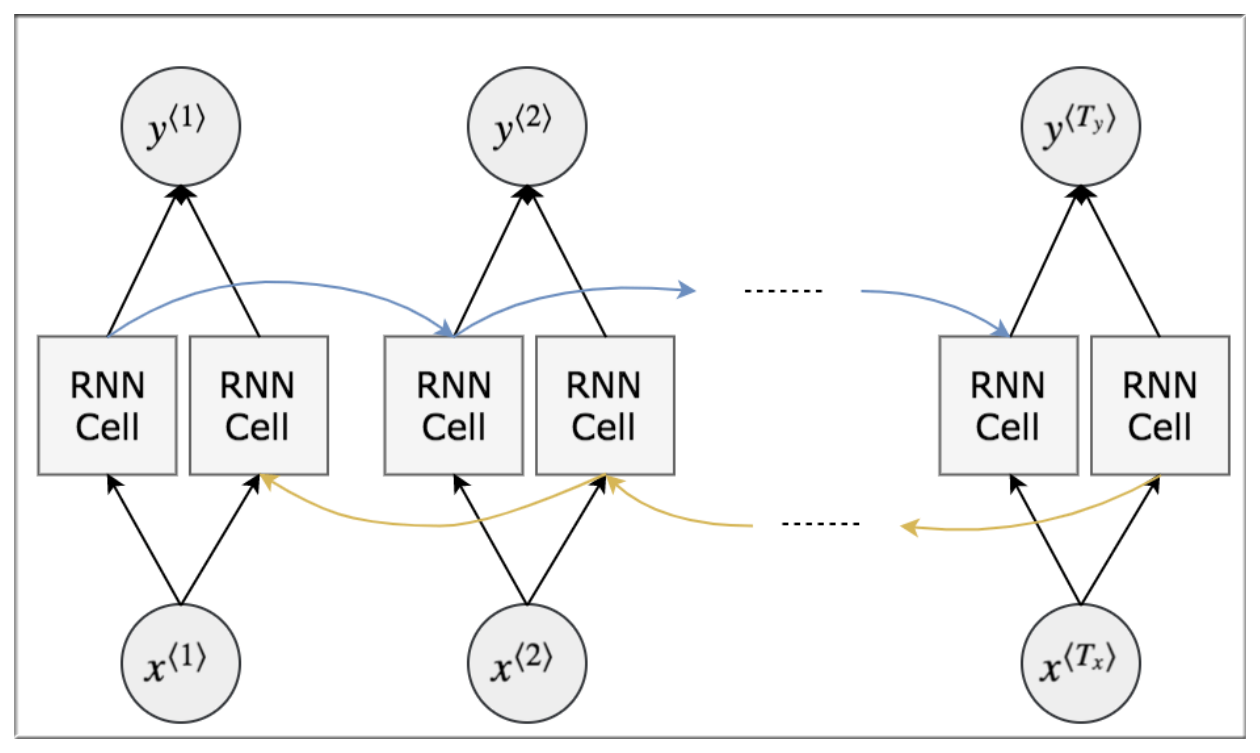
7. Deep RNNs
深层,顾名思义就是层次增加。如下图是深层循环神经网络的示意图
横向表示时间展开,纵向则是层次展开。
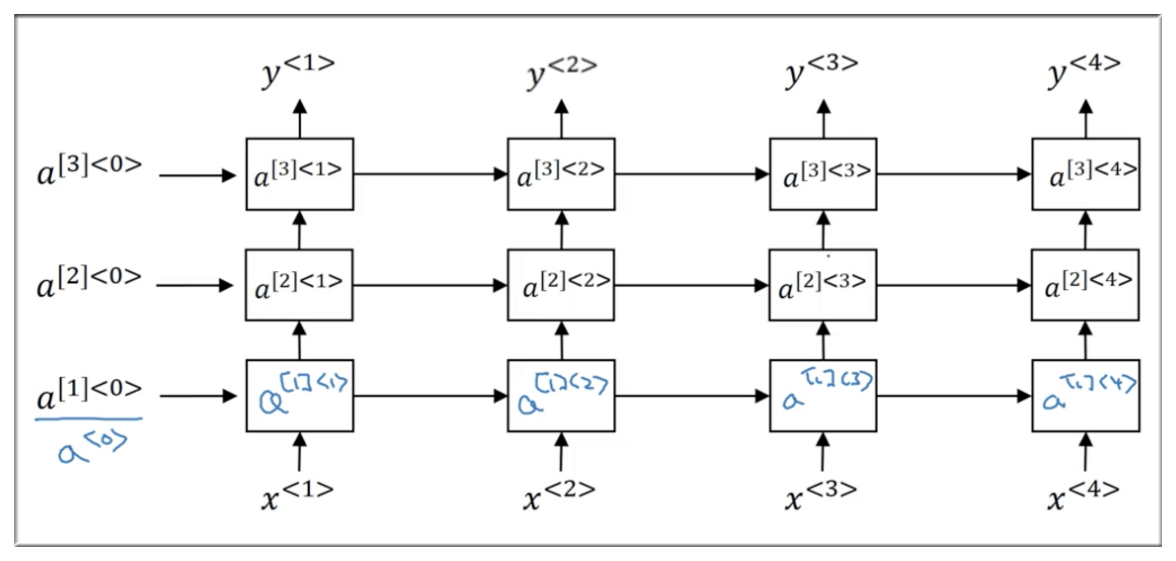
注意激活值的表达形式有所改变,以 a^{\[1\]<0>} 为例进行解释:
- [1] 表示第一层
- <0> 表示第一个激活值
另外各个激活值的计算公式也略有不同,以 a^{\[2\]<3>} 为例,其计算公式如下:
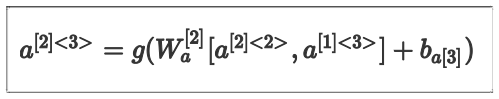


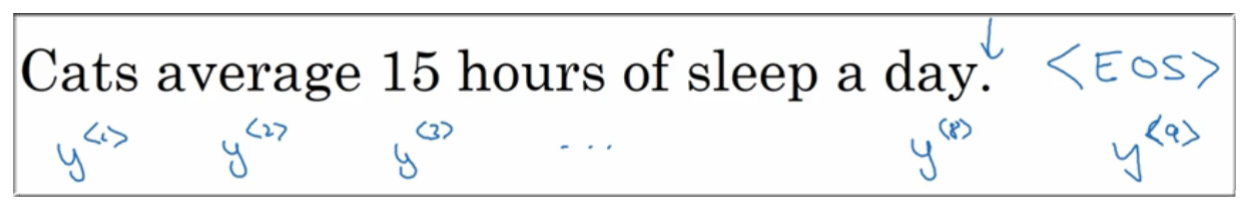
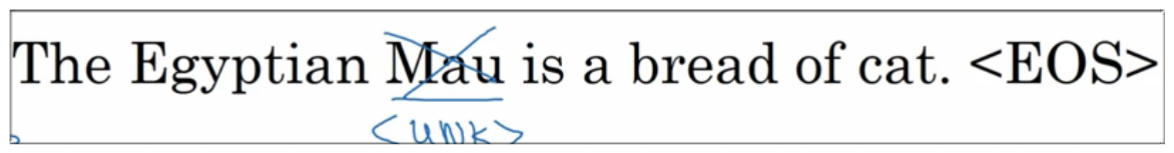
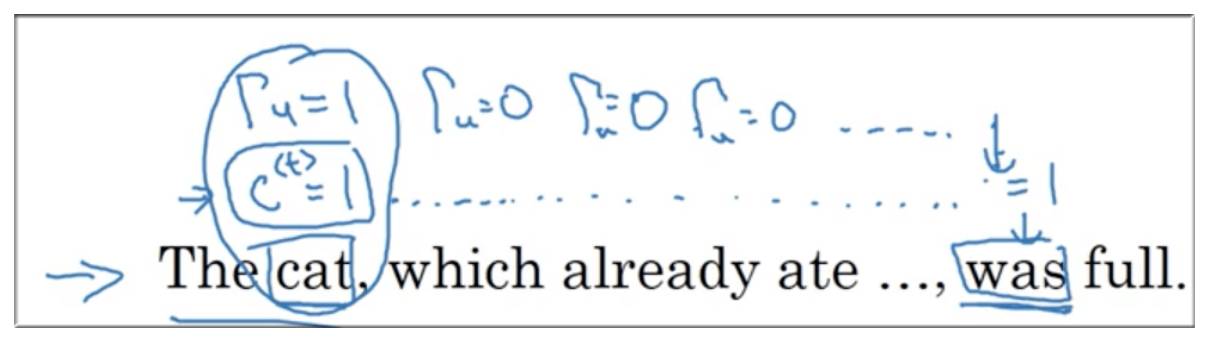




Checking if Disqus is accessible...