K-means

blairchen

data-science

Publish：Dec 18, 2018

views

在数据挖掘中， k-Means 算法是一种 cluster analysis 的算法，其主要是来计算数据聚集的算法，主要通过不断地取离种子点最近均值的算法。

1. 问题

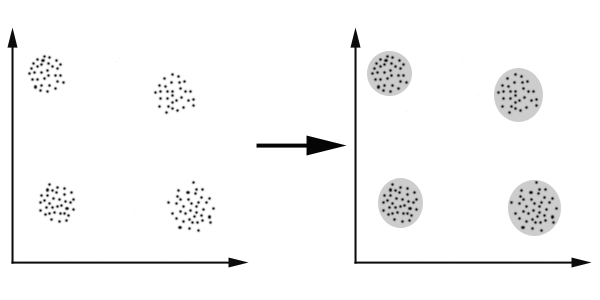
K-Means算法主要解决的问题如下图所示。我们可以看到，在图的左边有一些点，我们用肉眼可以看出来有四个点群，但是我们怎么通过计算机程序找出这几个点群来呢？于是就出现了我们的K-Means算法.

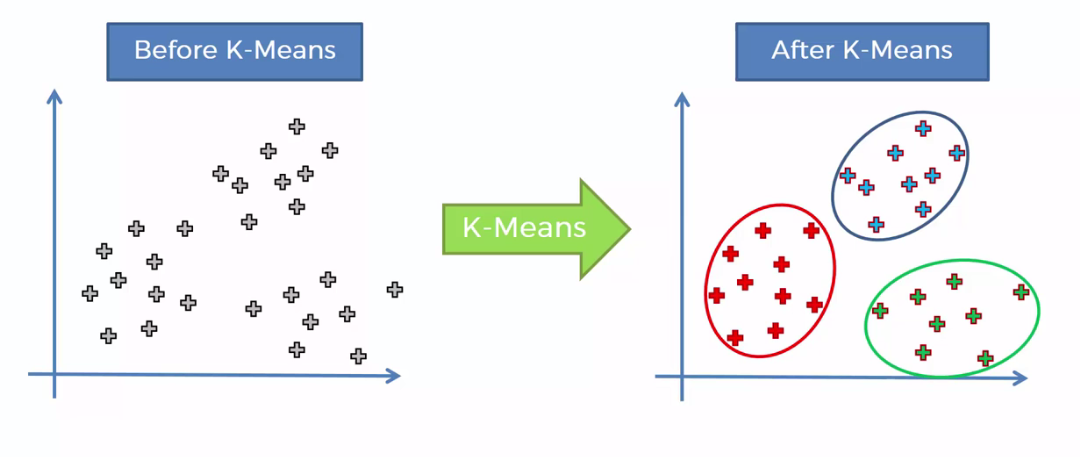
K均值聚类的基本思想是，通过迭代方式寻找K个簇(Cluster)的一种划分方案，使得聚类结果对应的代价函数最小。特别的，代价函数可以定义为各个样本距离所属簇中心点的误差平方和

2. 算法概要

这个算法其实很简单，如下图所示：

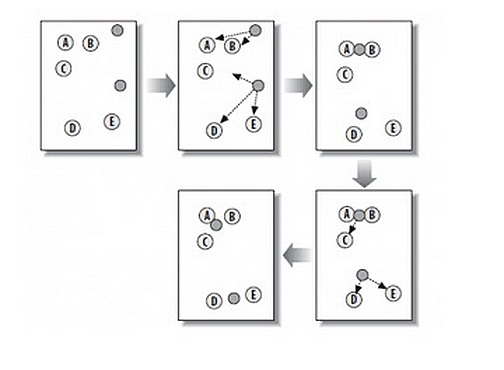
从上图中，我们可以看到，A, B, C, D, E 是五个在图中点。而灰色的点是我们的种子点，也就是我们用来找点群的点。有两个种子点，所以K=2。

然后，K-Means的算法如下：

1). 随机在图中取K（这里K=2）个种子点。

2). 然后对图中的所有点求到这K个种子点的距离，假如点Pi离种子点Si最近，那么Pi属于Si点群。（上图中，我们可以看到A,B属于上面的种子点，C,D,E属于下面中部的种子点）.

3). 接下来，我们要移动种子点到属于他的“点群”的中心。（见图上的第三步）.

4). 然后重复第2）和第3）步，直到，种子点没有移动（我们可以看到图中的第四步上面的种子点聚合了A,B,C，下面的种子点聚合了D，E）。

这个算法很简单。

3. K-Means 具体步骤

(1). 数据预处理、归一化、离群点处理。

(2). 随机选择 K 个簇中心，记为 ${\mu\_1}^{(0)}, {\mu\_2}^{(0)}, {\mu\_3}^{(0)}, ..., {\mu\_k}^{(0)}$

(3). 定义代价函数 :

(4). 令 t=0,1,2,… 为迭代轮数，重复下面的过程知道 J 收敛:

对于每一个样本 $x\_i$ , 将其分配到距离最近的簇.

对于每一个类簇 $k$ , 重新计算该类簇的中心

4. K-Means 优缺点

Advantage：

对于大数据集，K均值高效且可伸缩，它的复杂度是 $O(NKt)$ ，接近于线性。其中 t是迭代轮数。

Disadvantage：

(1) 需要人工预设K值，且该值和真实数据分布未必吻合；

(2) 受初值和离群点的影响，每次的结果不稳定；

(3) 受初值影响，结果通常是局部最优；

(4) 无法很好地解决数据簇分布差别比较大的情况(如一类是另一类样本数量的100倍)；

(5) 不太适用于离散分布；样本点只能被划分到单一的类中。