- 理解如何搭建一个神经网络,包括最新的变体,例如残余网络。
- 知道如何将卷积网络应用到视觉检测和识别任务。
- 知道如何使用神经风格迁移生成艺术。
- 能够在图像、视频以及其他2D或3D数据上应用这些算法。
1. Computer vision
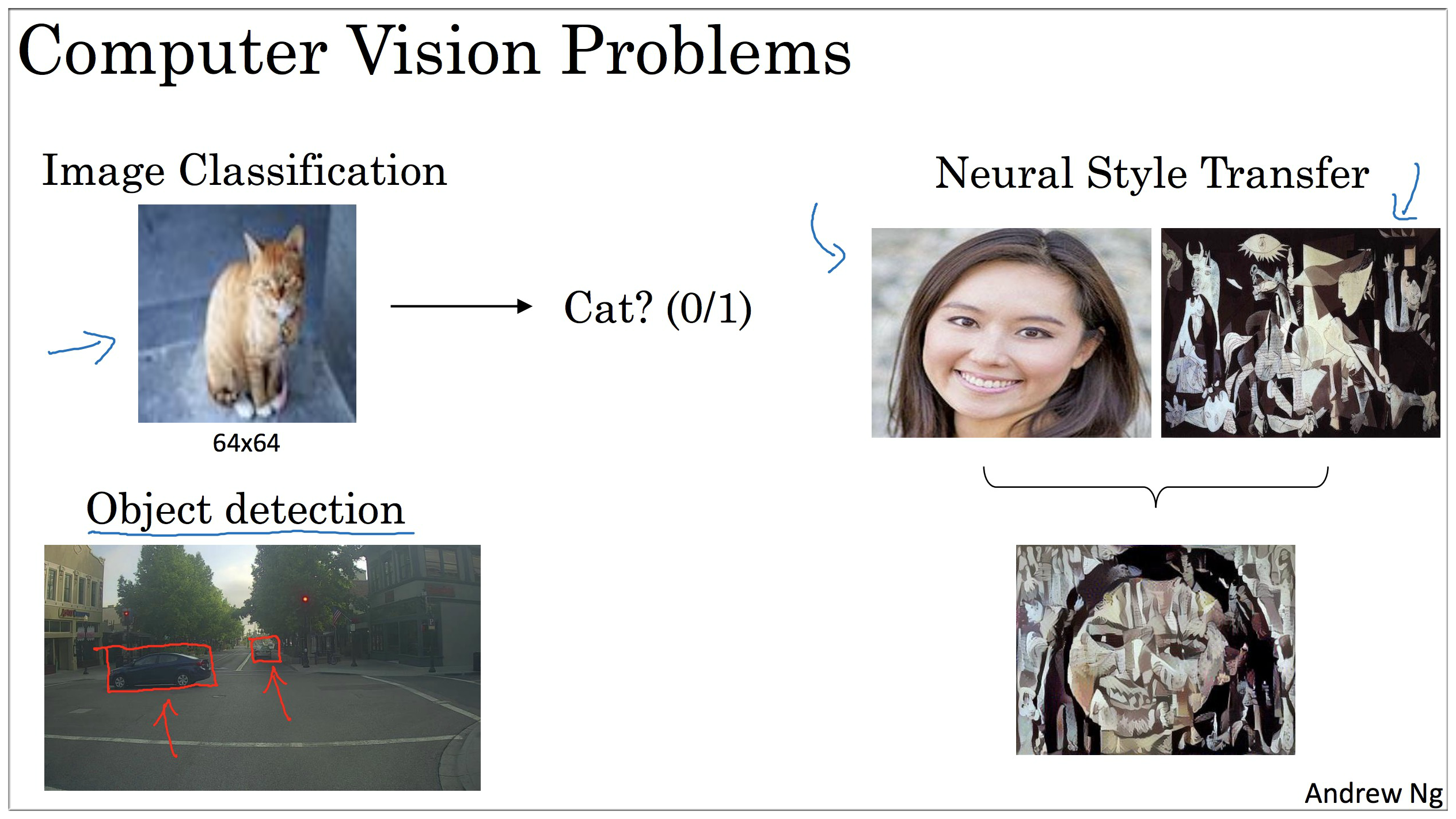
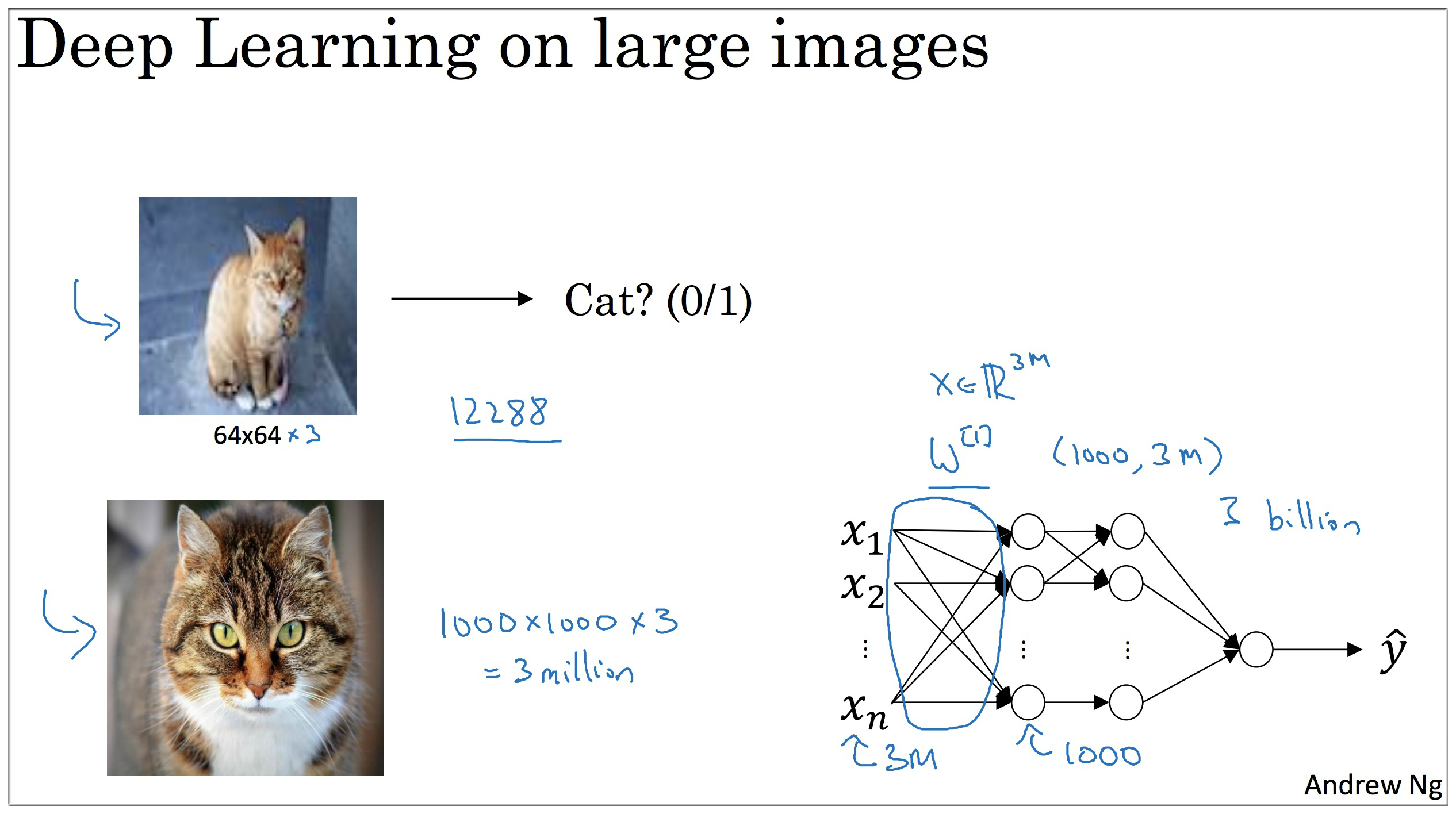
如图示,之前课程中介绍的都是 64 * 64 * 3的图像 (3 代表:因为每个图片都有3个颜色通道 channels, 12288 So , the input features has dimension 12288),而一旦图像质量增加,例如变成 1000 * 1000 * 3 的时候那么此时的神经网络的计算量会巨大,显然这不现实。所以需要引入其他的方法来解决这个问题.
2. Edge detection example
使用边缘检测作为入门样例, you see how the convolution operation works.
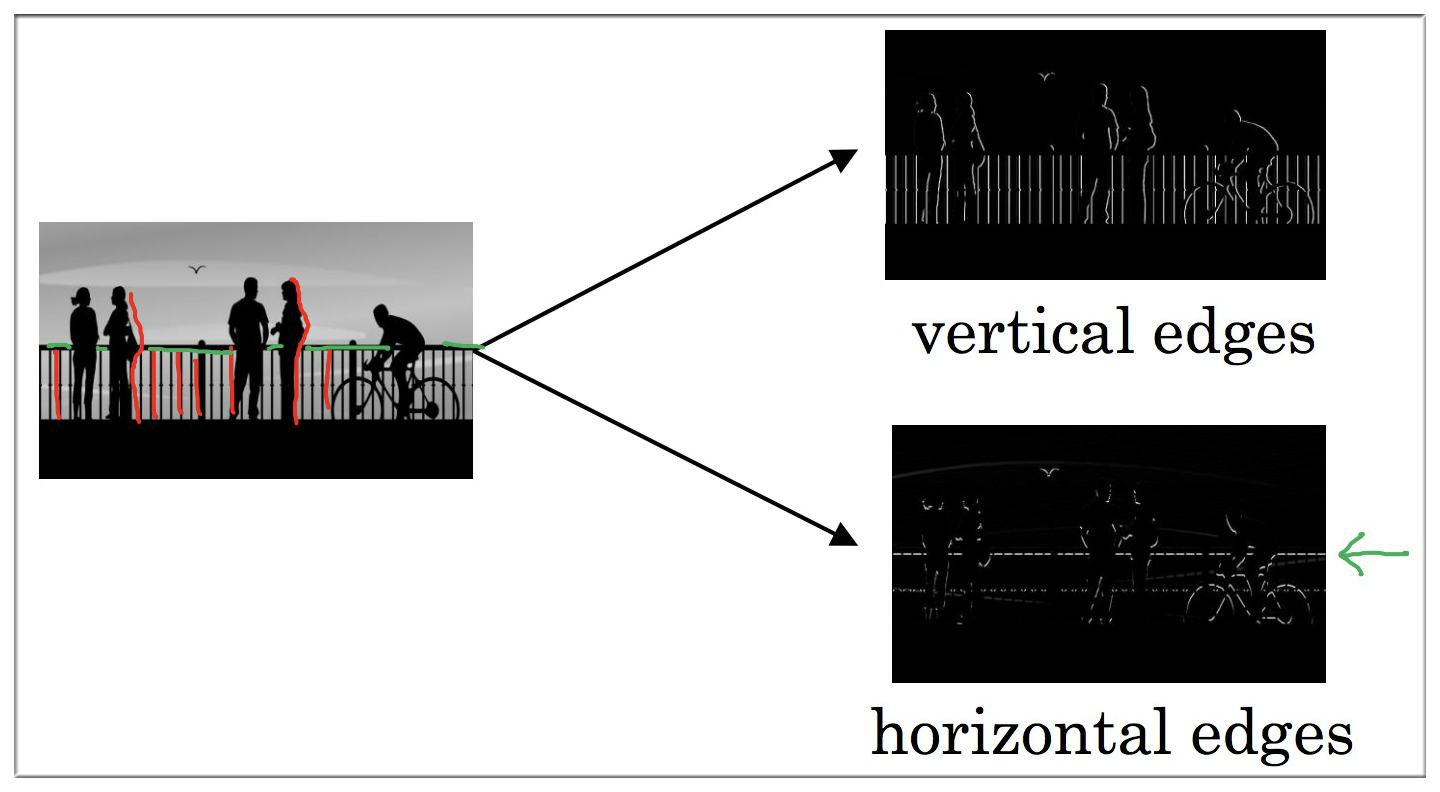
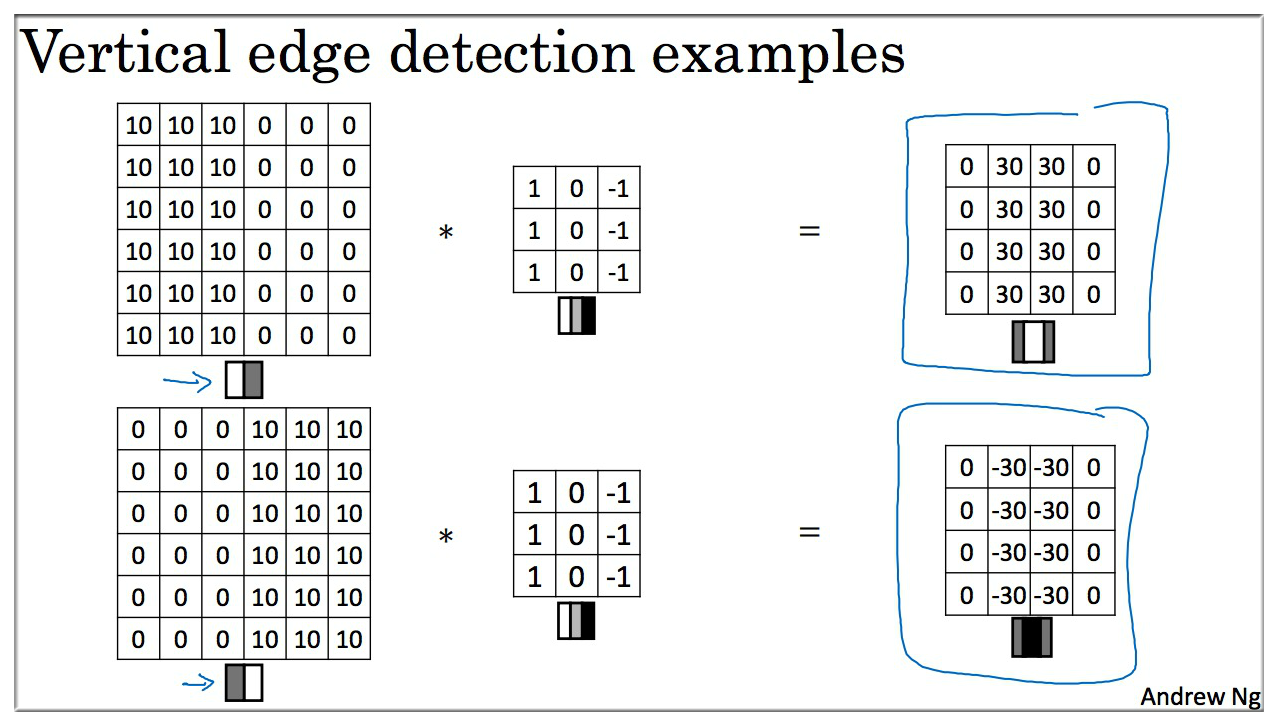
边缘检测可以是垂直边缘检测,也可以是水平边缘检测,如上图所示.
至于算法如何实现,下面举一个比较直观的例子:
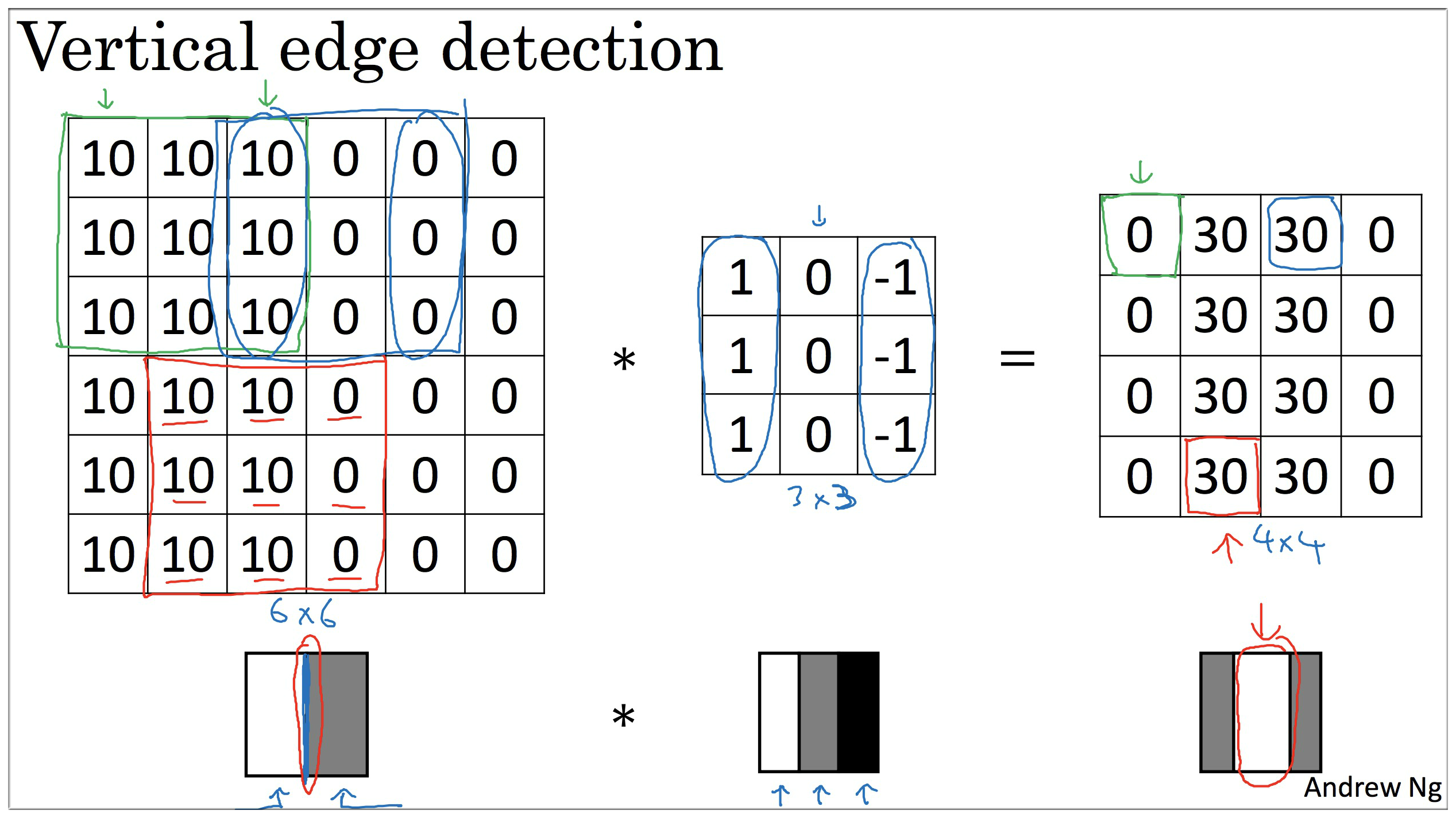
可以很明显的看出原来 6 * 6 的矩阵有明显的垂直边缘,通过 3 * 3 的过滤器 filter (也叫做 “核”)卷积之后,仍然保留了原来的垂直边缘特征,虽然这个边缘貌似有点粗,这是因为数据不够大的原因,如果输入数据很大的话这个不是很明显了.
关于用编程语言实现:python / tensorflow / keras 等,都有一些函数来实现卷积运算.
3. More edge detection
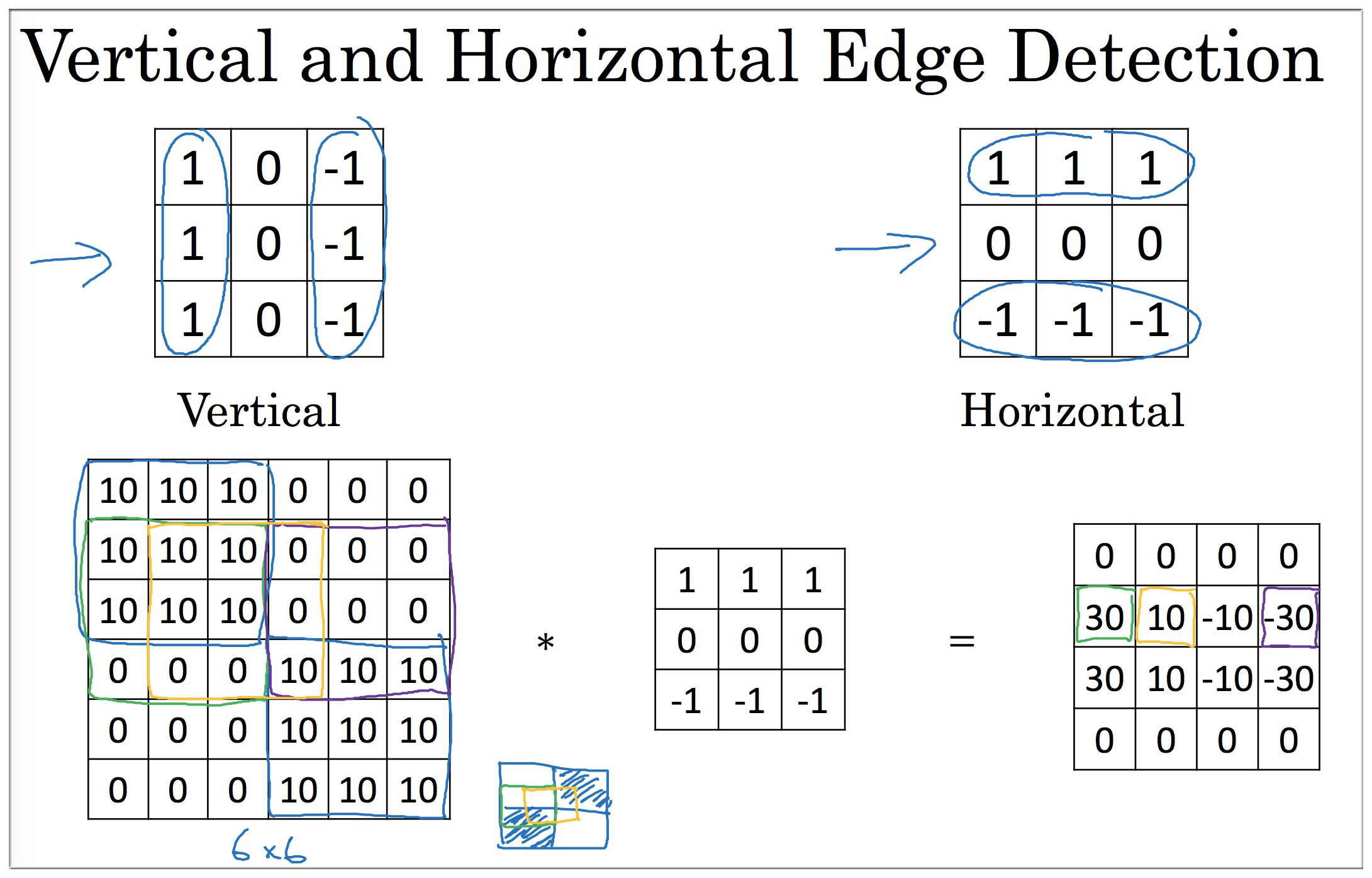
除了上面的垂直,水平边缘检测,其实也可以检测初颜色过度变化,例如是亮变暗,还是暗变亮?
**在计算机视觉的历史上,层曾经公平的争论过哪些什么样的 filter 数字组合才是最好的:
**
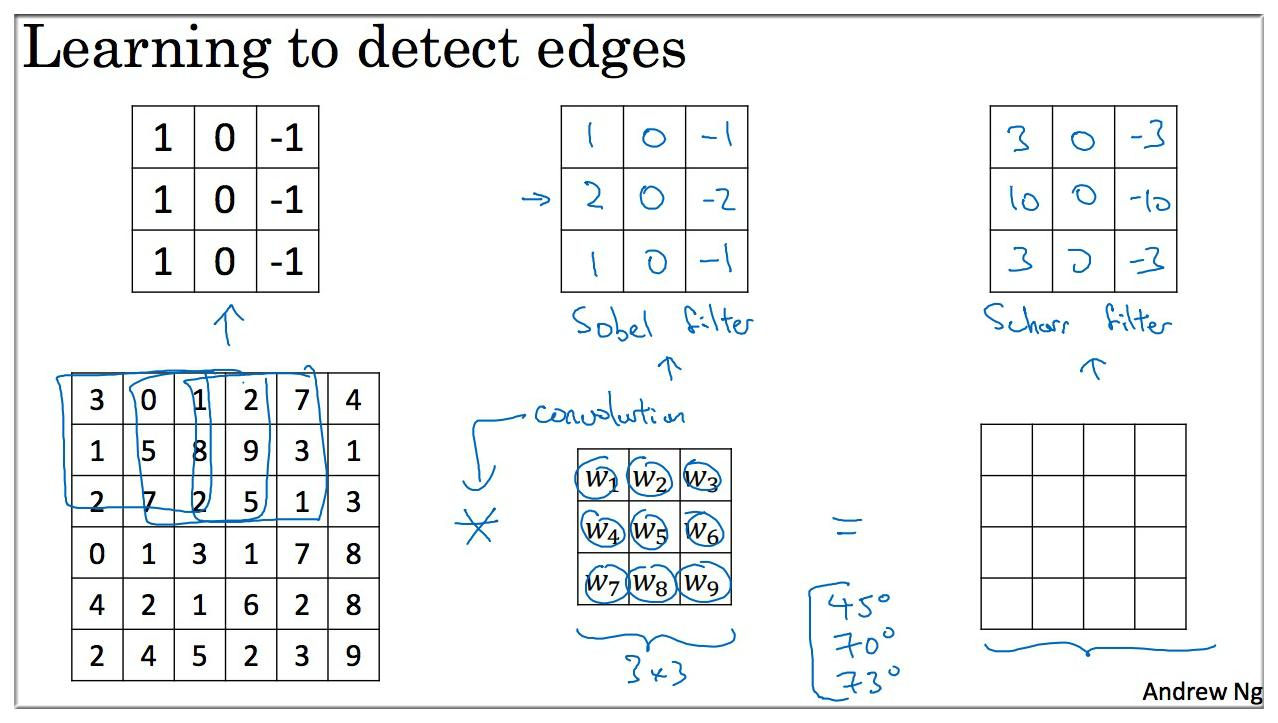
下面是一些常见的过滤器,第二个是
Sobel filter,具有较强的鲁棒性,第三个是Schoss filter.
| Filter | desc |
|---|---|
| Sobel Filter | it puts a little bit more weight to the central row 增加了中间一行的权重 |
| Schoss Filter | 实际它也是一种垂直边缘检测 翻转90度,它就变为水平边缘检测 |
| Other Filter | 9个参数也可以通过学习(反向传播)的方式获得 |
其实过滤器的9个参数也可以通过学习(反向传播)的方式获得,虽然比较费劲,但是可能会学到很多其他除了垂直,水平的边缘特征,例如 45°,70° 等各种特征.
4. Padding
由前面的例子, 卷积的方法,有2个缺点:
每经过一次卷积计算,原数据都会减小,但有时我们并不希望这样。举个比较极端的例子:假设原数据是 30 * 30 的一只猫的图像,经过10次卷积 (过滤器是3 * 3) 后,最后图像只剩下了 10 * 10 了 😳😳
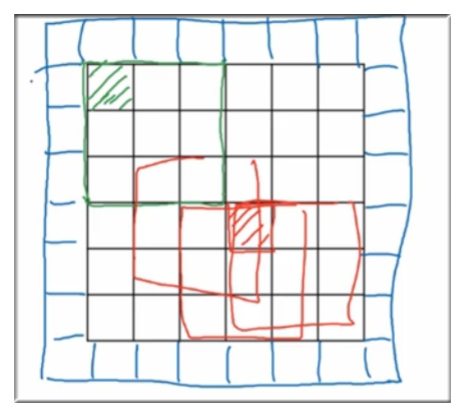
由卷积的计算方法可知,图像边缘特征计算次数显然少于图像中间位置的像素点,如下图示 (绿色的位置明显是冷宫), 图像边缘的大部分信息都丢失了.
4.1 运用 Padding 的原因
原来的 6 * 6 填充后变成了 8 * 8,此时在经过一次卷积得到的仍旧是 6 * 6 的矩阵。
下面总结一下卷积之后得到矩阵大小的计算方法,假设:
| Title | Size | desc |
|---|---|---|
| 原数据 | n \* n | 矩阵 n \* n |
| Filter | f \* f | 过滤器 |
| Padding | p \* p | 填充数量 |
| 综上: | 得到的矩阵大小 |
padding 后,虽然边缘像素点仍旧计算的比较少,但是这个缺点至少一定程度上被削弱了.
4.2 如何 padding 的大小
| Type | desc | Size |
|---|---|---|
| Valid convolutions | 不添加 padding | |
| Same convolutions | Pad so that output size is the same as the input size. 保持原图像矩阵的大小 |
满足 即 , 为了满足上式, 一般奇数 |
5. Strided convolutions
过滤器 纵向、横向 都需要按 步长 来移动,如图示:
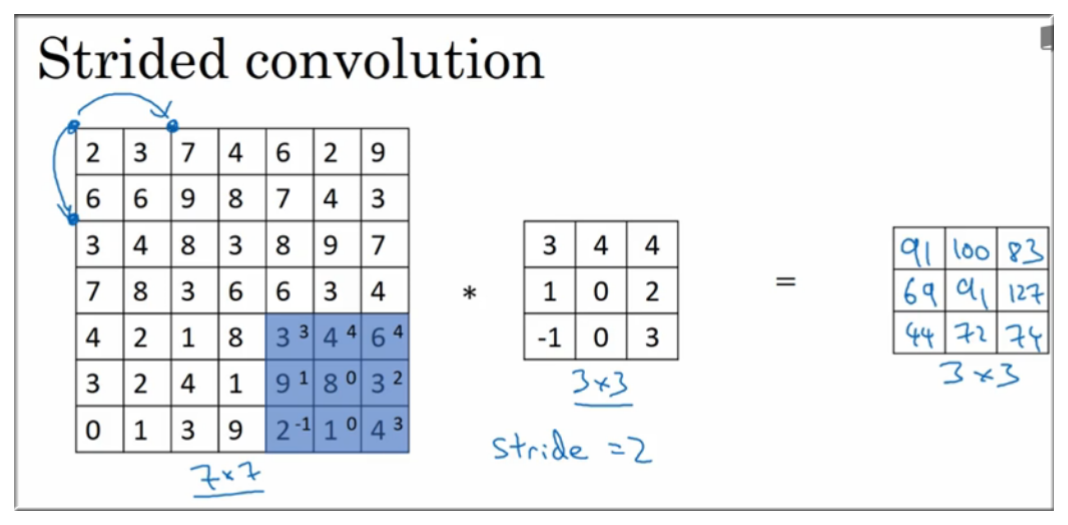
结合之前的内容,输出矩阵大小计算公式方法为,假设:
| Title | Size | desc |
|---|---|---|
| 原数据 | n \* n | 矩阵 n \* n |
| Filter | f \* f | 过滤器 |
| Padding | p \* p | 填充数量 |
| Stride | s \* s | 步长 |
| 综上: | 得到的矩阵大小是 | ⌊⌋ * ⌊⌋ |
⌊⌋: 向下取整符号 ⌊59/60⌋ = 0
⌈⌉: 向上取整符号 ⌈59/60⌉ = 1
6. Convolutions Over Volumes
这一节用立体卷积来解释
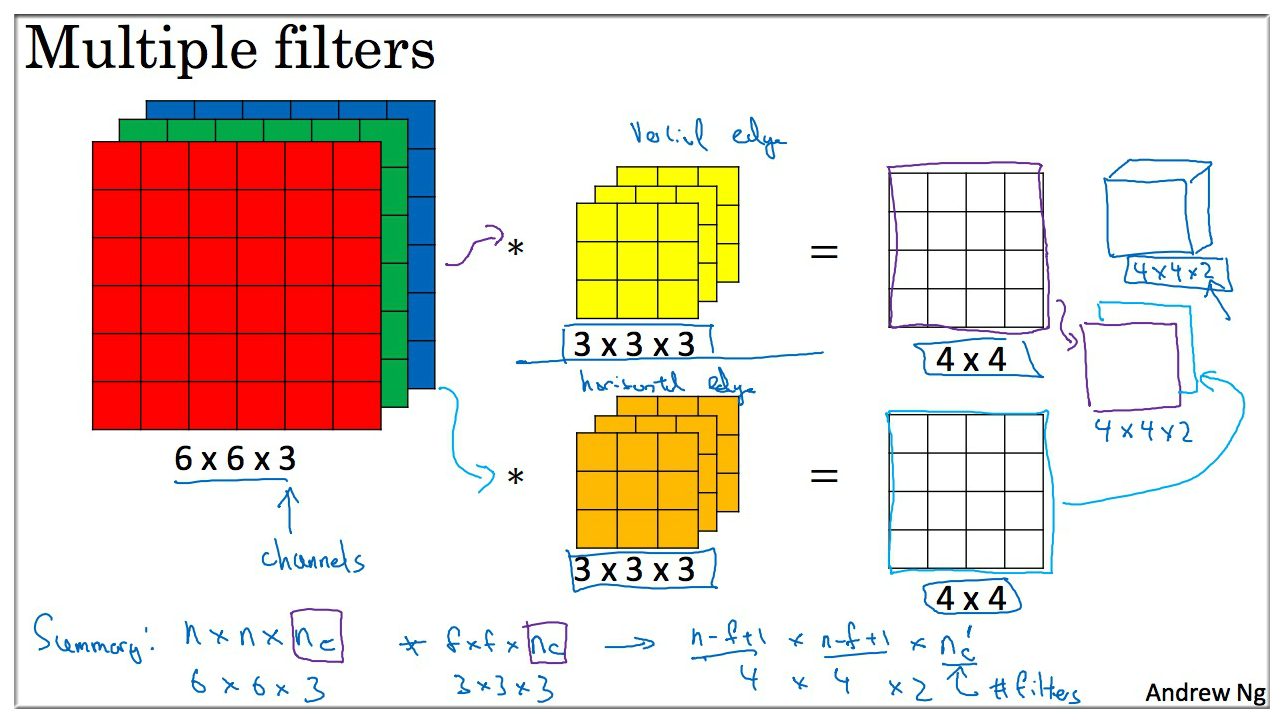
如图:
- 输入矩阵是 6 \* 6 \* 3 (height * width * channels), 过滤器是 3 \* 3 \* 3,计算方法是一一对应相乘相加
- 最后得到 4 \* 4 的二维矩阵.
有时可能需要检测 水平边缘 或 垂直边缘,或 其他特征,所以我们可以使用多个过滤器。上图则使用了两个过滤器 (黄色和橘黄色),得到的特征矩阵大小为 4 \* 4 \* 2.
Filter 数字组合参数的选择不同,你可以得到不同的特征检测器.
7. One Layer of CNN Example
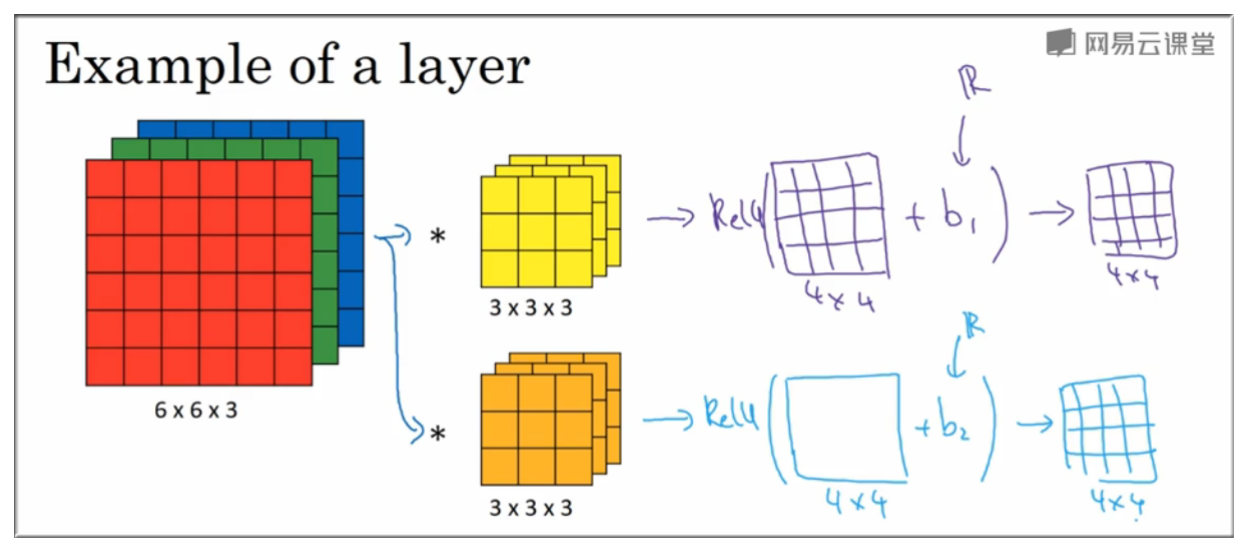
如图示得到 4 \* 4 的矩阵后还需要加上一个偏差 (Python 广播机制),之后还要进行非线性转换,即用 ReLU 函数.
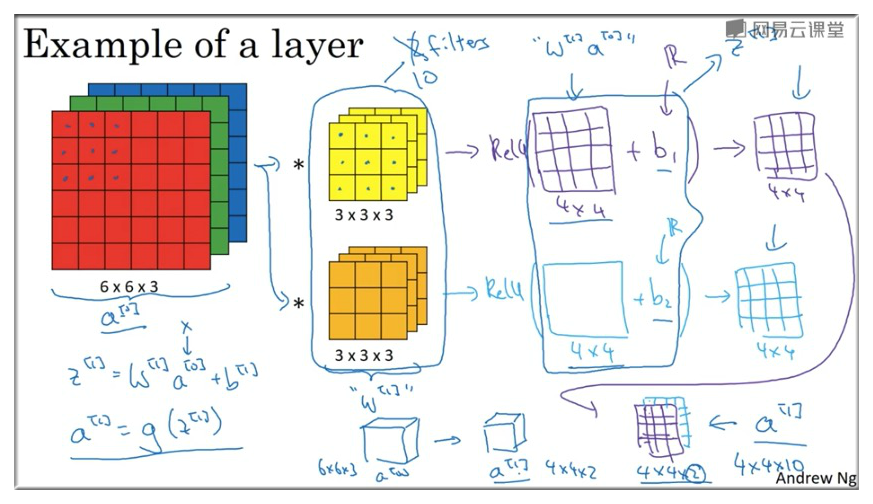
因此假如在某一卷积层中使用了 10 个 3 \* 3 的 Filter 过滤器,那么一共有 (3\*3+1)\*10=280 个参数.

下面总结了各项参数的大小和表示方法:
| Title | Formula | desc |
|---|---|---|
| 输入矩阵 | n\_H^{l-1} \* n\_W^{l-1} \* n\_c^{l-1} | height \* width \* channels = 6 \* 6 \* 3 |
| 过滤器大小 | ||
| Padding | ||
| Stride | 步长 | |
| Each Filter is | f^{l} \* f^{l} \* n\_c^{[l-1]} | 3 \* 3 \* 3 , 每一卷积层的过滤器的通道的大小 = 输入层的通道大小 |
| Activations 激活函数 | = n\_H^{l} \* n\_W^{l} \* n\_c^{l} | = m \* n\_H^{l} \* n\_W^{l} \* n\_c^{l},(个例子) |
| 权重 weight | f^{l} \* f^{l} \* n\_c^{[l-1]} \* n\_c^{[l]} | Filter \* 过滤器个数 过滤器的个数 = 输出层的通道的大小 |
| 偏差 bias | 1 \* 1 \* 1 \* n\_c^{[l]} | |
| 输出矩阵 | n\_H^{l} \* n\_W^{l} \* n\_c^{l} | height \* width \* channels |
| Output | 输出层与输入层计算公式 |
8. A Simple Convolution Network
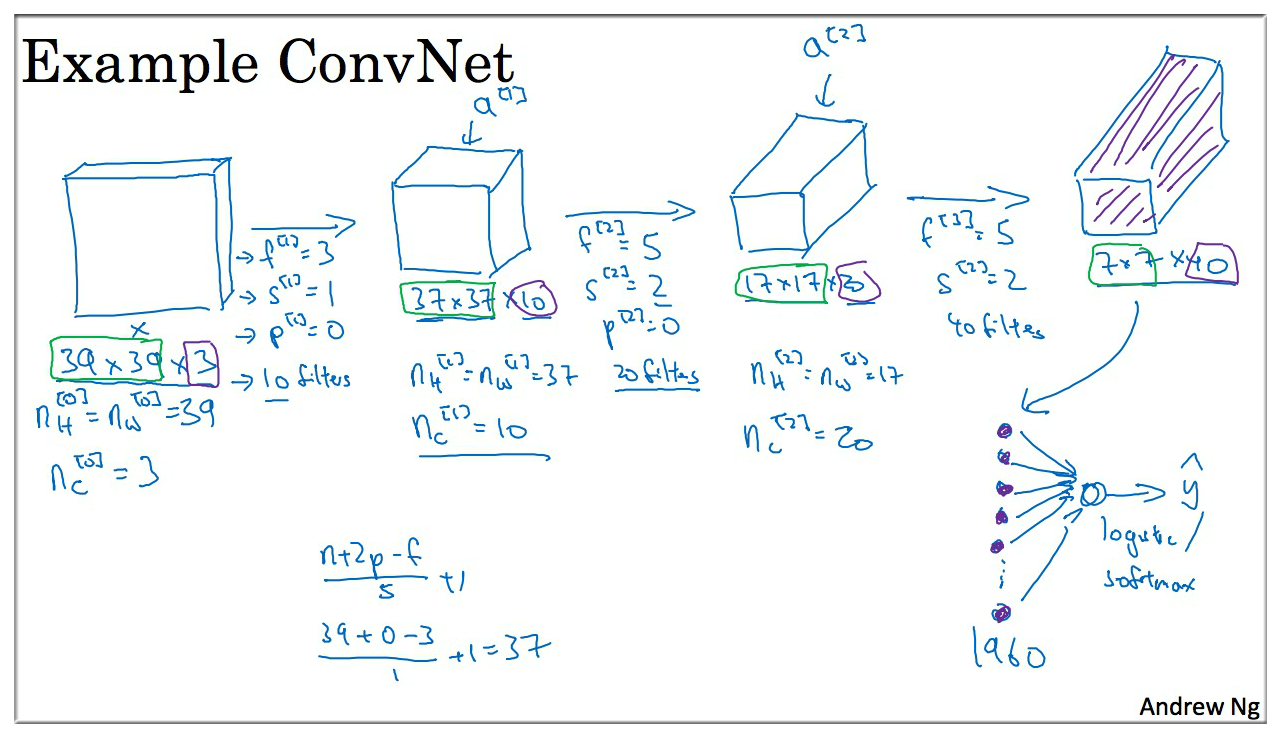
上图简单介绍了卷积网络的计算过程,需要再介绍的一点是最后一层的全连接层,即将 7 \* 7 \* 40 的输出矩阵展开,得到 个节点,然后再采用 Softmax 来进行预测.
一般的 CNN 中,每一层矩阵的 height 和 width 是逐渐减小的,而 channel 则是增加的 ( 在增加, 和 在减少).
CNN 中常见的 3 种类型的 layer:
- Convolution (Conv 卷积层)
- Pooling (Pool 池化层)
- Fully connected (FC 全连接层)
9. Pooling Layers
使用池化层来缩减模型的大小,提高计算速度,同时提高提取特征的鲁棒性.
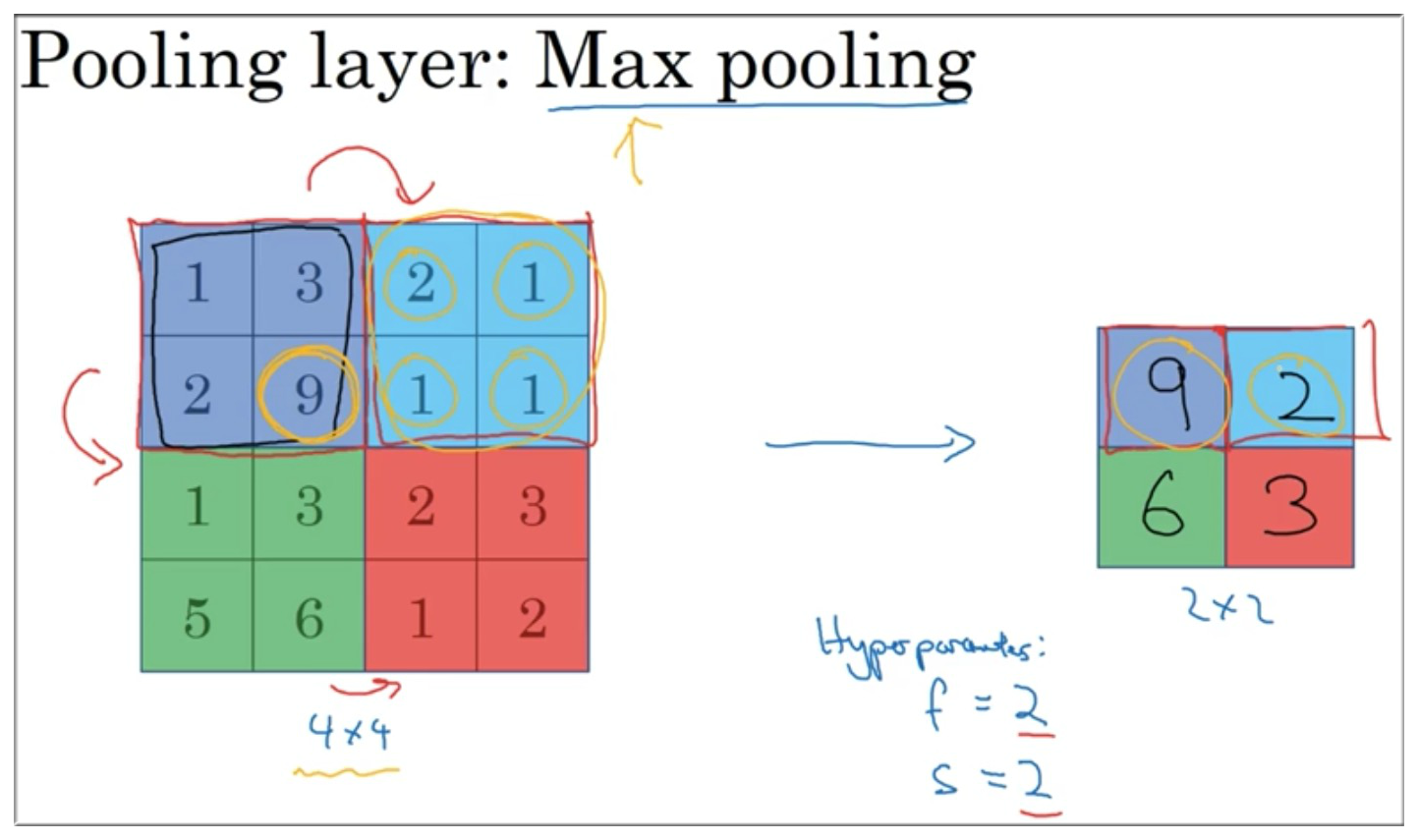
最大池化的直观理解:
你可以把上面 4 \* 4 输入看做是某些特征的集合 (也许不是),也就是神经网络中某一层的反激活值,数字大意味着可能提取了某些特定特征. 左上象限具有这个特征,可能是一个垂直边缘. or maybe an eye, 显然左上象限具有这个特征.
最大化操作的功能就是只要在任何一个象限内提取到某个特征,它就会保留在最大池化的输出里. 最大化操作的实际作用就是:如果在 Filter 中提取到某个特征 那么保留其最大值. 如果没有提取到这个特征,比如说 右上象限 中,那么其最大值也还是很小.
Max Pooling的超级参数 , 是最常用的,效果相当于高度和宽度缩减一半.Max Pooling很少用 padding, by far, is ,Average Pooling 这个用的不多,这个也会加入更多的计算量.
10. A CNN Example
在 Andrew Ng 的课件中将 Conv layer 和 Pooling layer 合并在一起视为一层,因为池化层没有参数 (因为池化层的过滤器 无参数,有超参数,而且其大小可以事先确定好)。 但是在其他文献中有可能会把池化层算成单独的层,所以视情况而定。
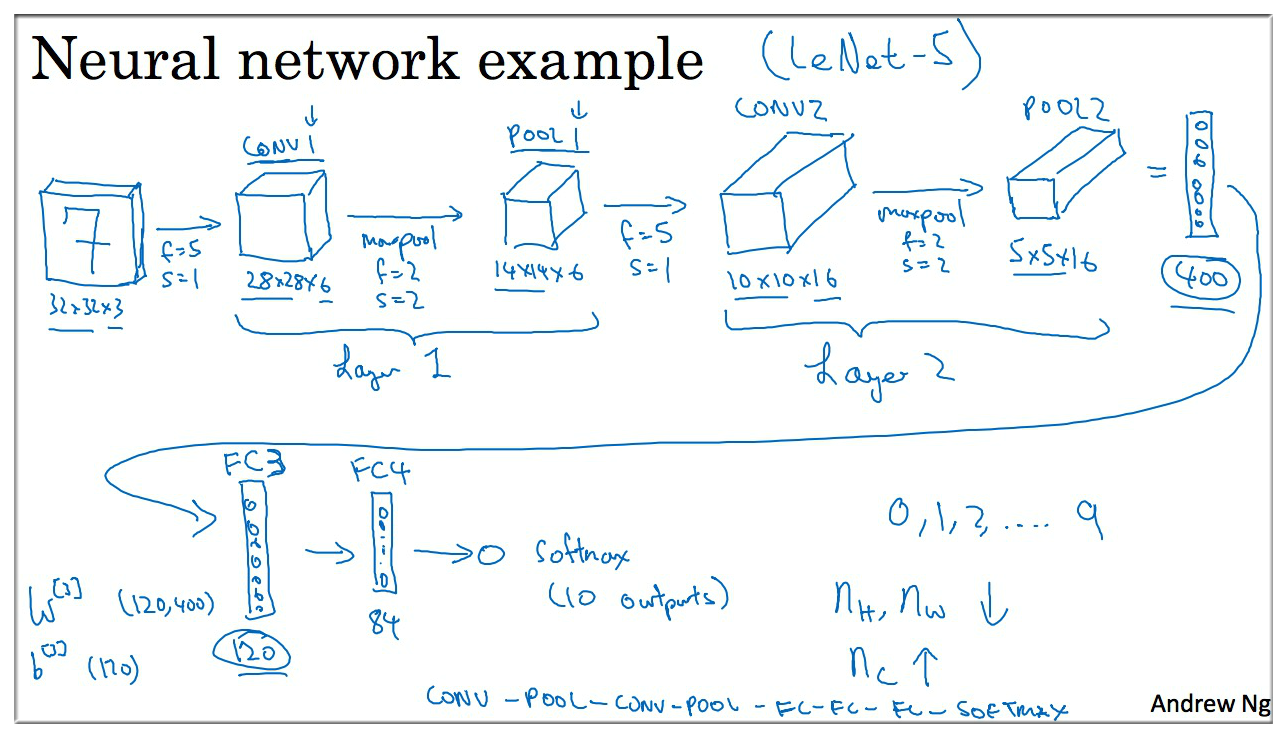
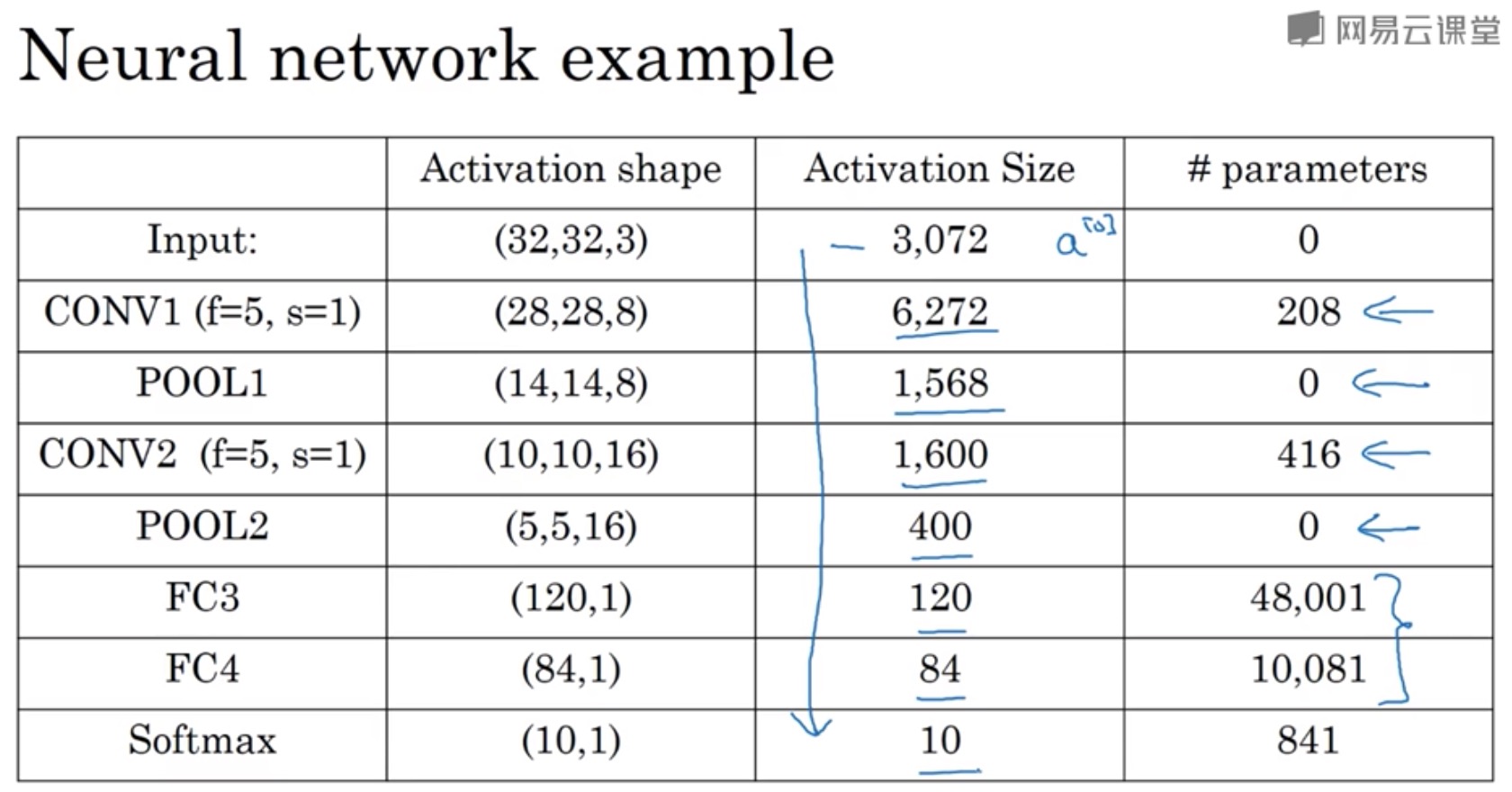
池化层参数个数为 0,卷积层参数个数一般多,fully connected layer 全连接层 参数很多.
11. Why Convolutions ?
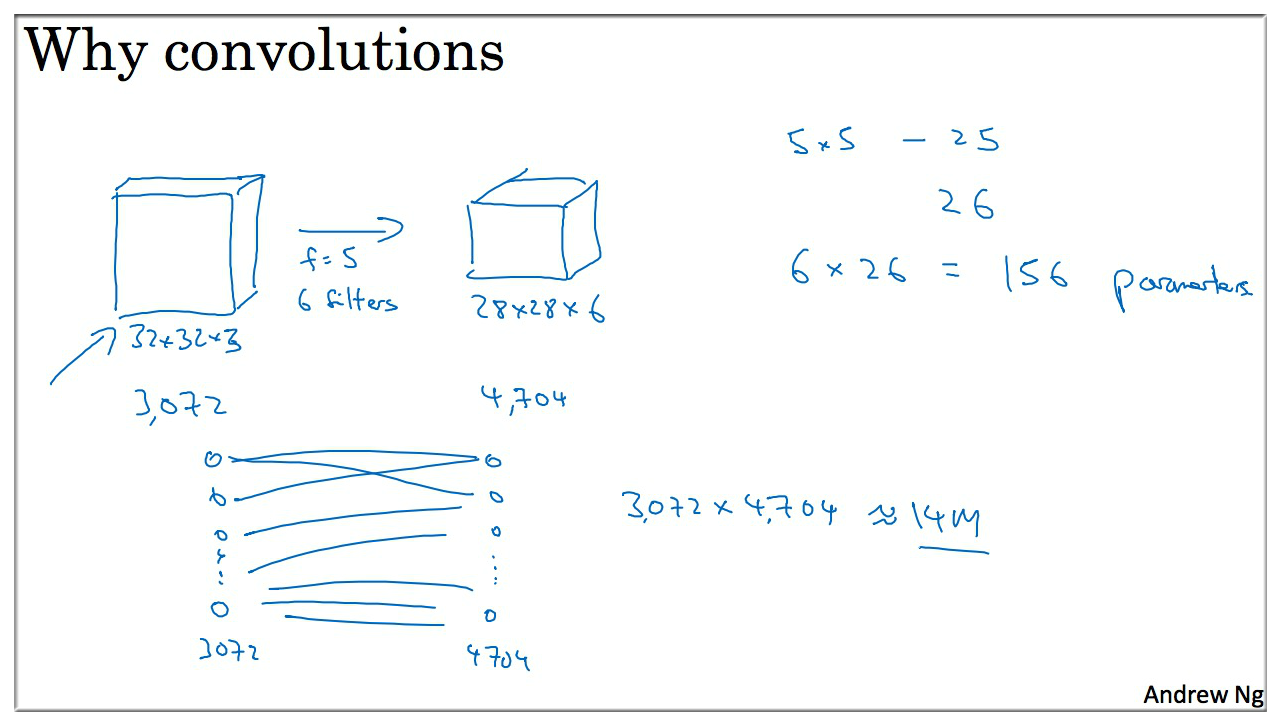
卷积 相比于 FC全连接 的好处最直观的就是使用的参数更少,参数共享 和 稀疏连接:
11.1 Parameter sharing
特征检测如垂直边缘检测如果适用于图片的某个区域,那么它也可能适用于图片的其他区域,也就是说如果你用一个 3 \* 3 的 Filter 检测垂直边缘. 那么图片的左上角区域以及旁边的各个区域都可以使用这个 3 \* 3 的过滤器. 每个特征检测器以及输出都可以在输入图片的不同区域中使用同样的参数,以便提取垂直边缘或其他特征,它不仅适用于边缘特征这样的低阶特征,同样适用于高阶特征. 例如:提取脸上的眼睛 等或者其他对象. 这种是整张图片共享特征检测器 提取效果也很好
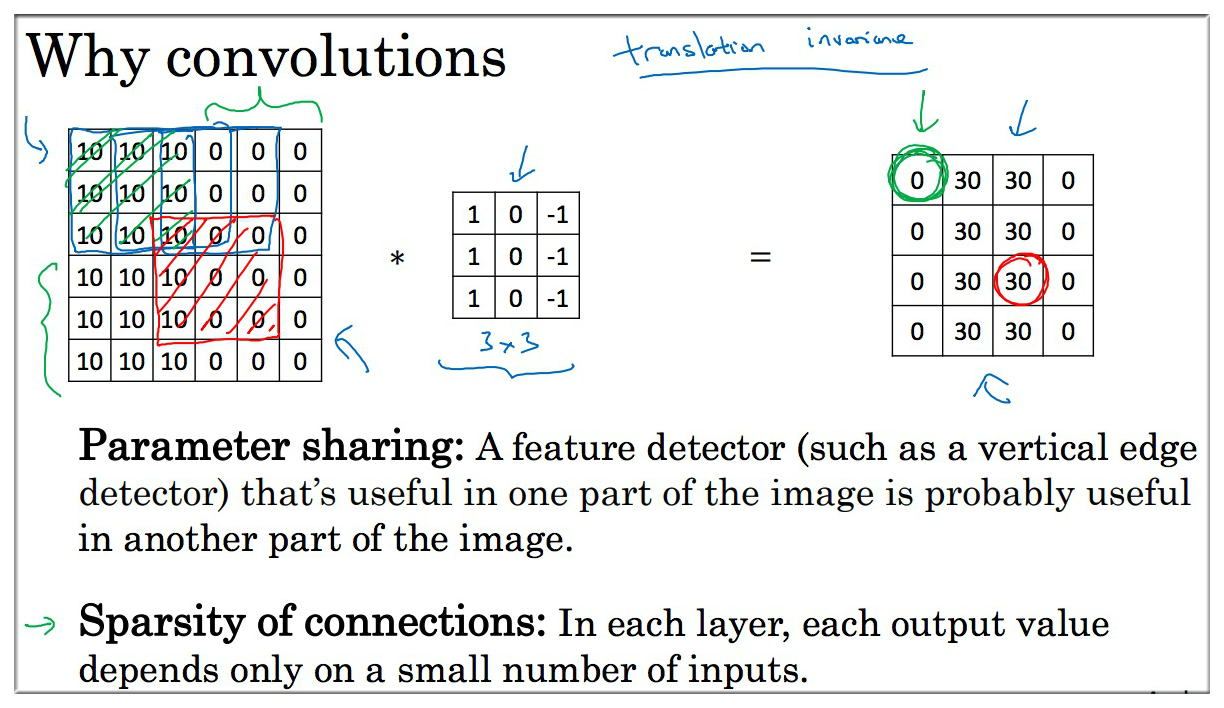
11.2 Sparsity of Connections
右边图 的边缘,仅与 36 个输入特征中的 9 个相连接, 而且其他像素值都不会对输出产生任何影响, 这就是稀疏连接的概念. 某个输出点,看上去只有这 9 个输入特征与输出相连接. 其他像素对输出没有任何影响. 神经网络可以通过这两种机制减少参数. 以便于我们用更小的训练集训练它,从而预防过度拟合. (卷积有一个平移不变属性)
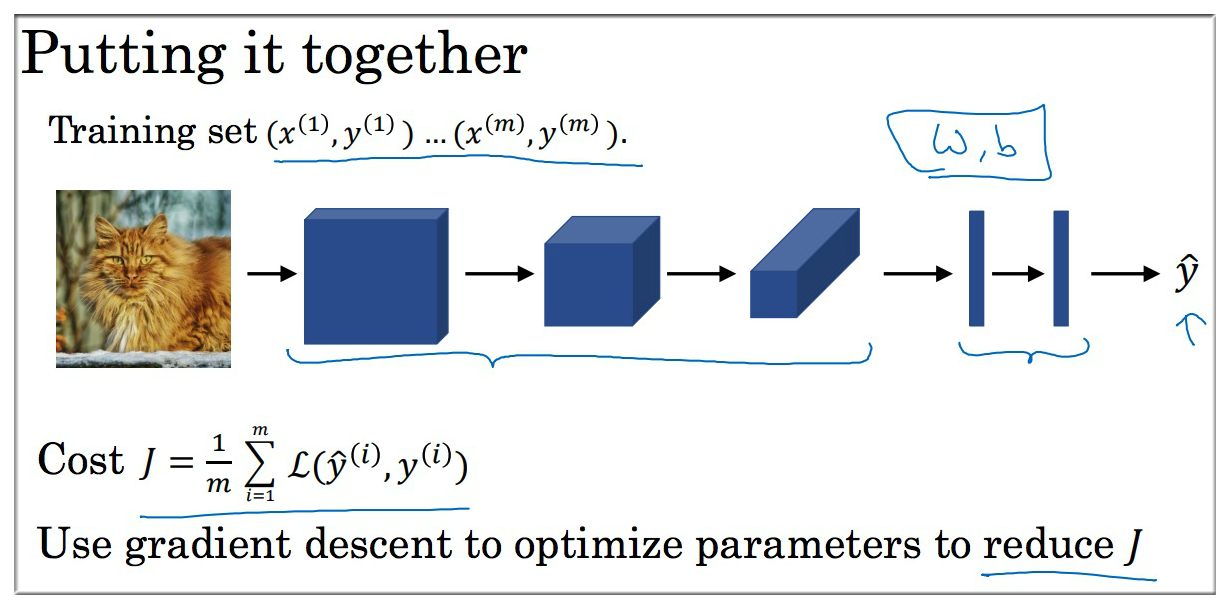
综上这些就是卷积神经网络 CNN 表现良好的原因.






Checking if Disqus is accessible...