Coursera Week 1 - Linear Algebra Matrices And Vectors

blairchen

data-science

Publish：Sep 30, 2016

views

coursera week 1 - matrices and vectors

1. Matrix Elements

A = \begin{bmatrix} 1 & 2 \\\ 4 & 5 \\\ 7 & 8 \end{bmatrix} \tag{fmt.1 R^{32}}

$ A_{ij} = $ "$i, j$ entry" in the $i^{th}$ row, $j^{th}$ column

$ A_{32} = 8 $

2. Vector $A\_n$ n*1 matrix

y = \begin{bmatrix} 460 \\\ 232 \\\ 315 \\\ 178 \end{bmatrix} \tag{fmt.2}

$R^4$ 4 dimensional vector
$y\_i = i^{th} element$

2.1 math 1-indexed

y = \begin{bmatrix} y1 \\\ y2 \\\ y3 \\\ y4 \end{bmatrix} \tag{fmt.3}

2.2 machine-learning 0-indexed

y = \begin{bmatrix} y0 \\\ y1 \\\ y2 \\\ y3 \end{bmatrix} \tag{fmt.4}

3. Matrix Addition

\begin{bmatrix} 1 & 0 \\\ 2 & 5 \\\ 3 & 1 \end{bmatrix} + \begin{bmatrix} 4 & 0.5 \\\ 2 & 5 \\\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 5 & 0.5 \\\ 4 & 10 \\\ 3 & 2 \end{bmatrix}

4. Scalar Multiplication

3 \times \begin{bmatrix} 1 & 0 \\\ 2 & 5 \\\ 3 & 1 \end{bmatrix} = \begin{bmatrix} 3 & 0 \\\ 6 & 15 \\\ 9 & 3 \end{bmatrix}

5. Combination of Operands

3 \times \begin{bmatrix} 1 \\\ 4 \\\ 2 \end{bmatrix} + \begin{bmatrix} 0 \\\ 0 \\\ 5 \end{bmatrix} - \begin{bmatrix} 3 \\\ 0 \\\ 2 \end{bmatrix} / 3 = \begin{bmatrix} 2 \\\ 12 \\\ 31/3 \end{bmatrix}

6. Matrix Vector Multiplication

$\begin{bmatrix} 1 & 3 \\\ 4 & 0 \\\ 2 & 1 \end{bmatrix} \times \begin{bmatrix} 1 \\\ 5 \end{bmatrix} = \begin{bmatrix} 16 \\\ 4 \\\ 7 \end{bmatrix}$

Matrix Vector Multiplication Fmt :

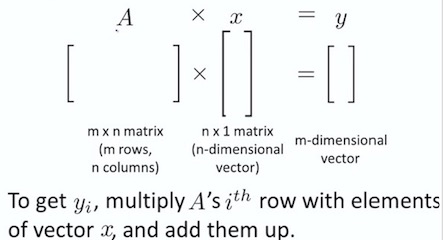
6.1 House sizes example

$h\_{\theta} (x) = -40 + 0.25 x$

\begin{bmatrix} 1 & 2104 \\\ 1 & 1416 \\\ 1 & 1534 \\\ 1 & 852 \end{bmatrix} \times \begin{bmatrix} -40 \\\ 0.25 \end{bmatrix} = \begin{bmatrix} -40 \times 1 + 0.25 \times 2104 \\\ ... \\\ ... \\\ ... \end{bmatrix}

7. Practice Example

\begin{bmatrix} 1 & 3 & 2 \\\ 4 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 3 \\\ 0 & 1 \\\ 5 & 2 \end{bmatrix} = \begin{bmatrix} 11 & 10 \\\ 9 & 14 \end{bmatrix}

$ A_{2 \times 3} \times A_{3 \times 2} = A_{2 \times 2} $

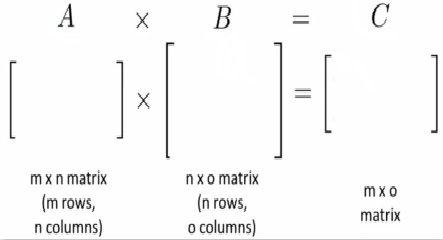
8. House Example

9. Matrix $A \times B \neq B \times A$

But, 结合律，可以的

$ A \times B \times C = (A \times B) \times C = A \times (B \times C) $

10. Identity Matrix

Denoted I (or I_{n*n}).

10.1 $2 \times 2$

\begin{bmatrix} 1 & 0 \\\ 0 & 1 \end{bmatrix} \tag{fmt.1 R^{32}}

10.2 $3 \times 3$

\begin{bmatrix} 1 & 0 & 0 \\\ 0 & 1 & 0 \\\ 0 & 0 & 1 \end{bmatrix} \tag{fmt.1 R^{32}}

$Z \times I = I \times Z = Z$

11. Matrix Inverse

$3 \times 3^{-1} = 1$

Not all numbers have an inverse.

if $A$ is an $m \times m$ matrix, and if it has an inverse

$A \times A^{-1} = A^{-1} \times A = I$

A = \begin{bmatrix} 3 & 4 \\\ 2 & 16 \\\ \end{bmatrix}

A^{-1} = \begin{bmatrix} 0.4 & -0.1 \\\ -0.05 & 0.075 \\\ \end{bmatrix}

$ A \times A^{-1} = I_{2 \times 2} $

I\_{2 \times 2} = \begin{bmatrix} 1 & 0 \\\ 0 & 1 \\\ \end{bmatrix}

12. Matrix Transpose

A = \begin{bmatrix} 1 & 2 & 0 \\\ 3 & 5 & 9 \\\ \end{bmatrix}

A^T = \begin{bmatrix} 1 & 3 \\\ 2 & 5 \\\ 0 & 9 \end{bmatrix}

Let $A$ be an $m \times n$ matrix, and let $B = A^T$.
Then $B$ is an $n \times m$ matrix, and $B\_{ij} = A\_{ji}$

updated on：May 2, 2022

machine-learning