Linear Regression Cost Function & Gradient descent
1. Linear Regression

2. Cost Function
Choose $\theta0,\theta_1$ so that $h{\theta} (x)$ is close to $y$ for our training examples ${(x, y)}$
| Title | fmt |
|---|---|
| Hypothesis | $h_{\theta} (x) = \theta_0 + \theta_1 x$ |
| Parameters | $\theta_0 、\theta_1$ |
| Cost Function | $J(\theta0,\theta_1) = {\frac {1} {2m}} \sum{i=1}^m (h_{\theta} (x^{i}) - (y^{i}))^2$ |
| Goal | $minimize J(\theta_0,\theta_1)$ |
3. Simplified Fmt
$\theta_0$ = 0
hypothesis function $h_{\theta} (x)$ cost function $J(\theta_1)$

4. Cost function visable
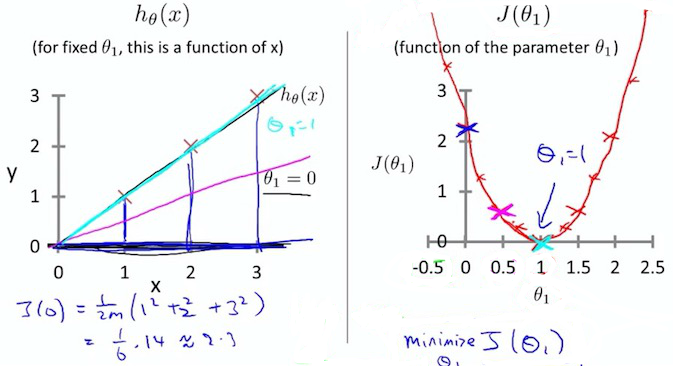
把 x, y 想象成向量,确定的向量,向量再想象为一个确定的数,总之它是一个二次函数,抽象的想一下,会不会理解
- contour plots
- contour figures
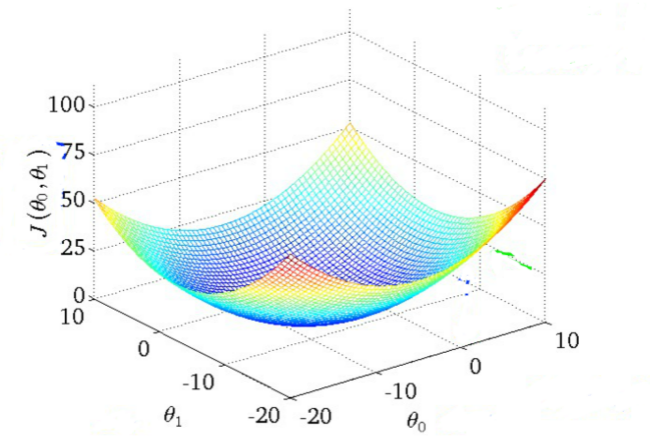
5. Gradient descent target
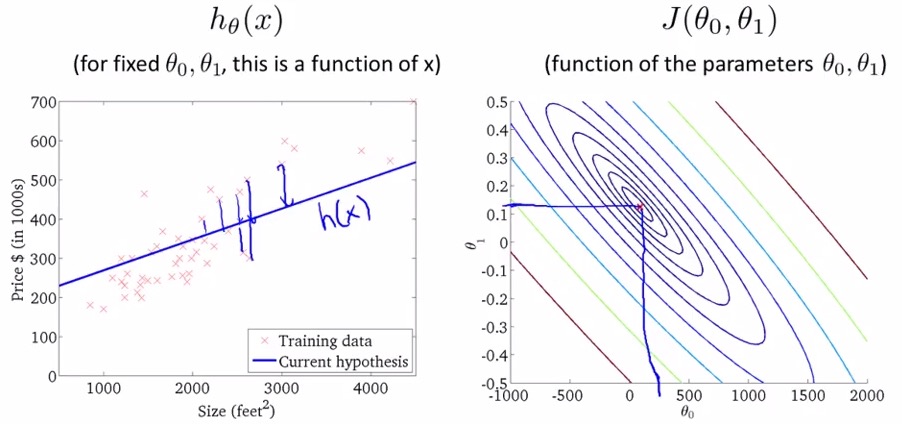
6. Gradient descent visable
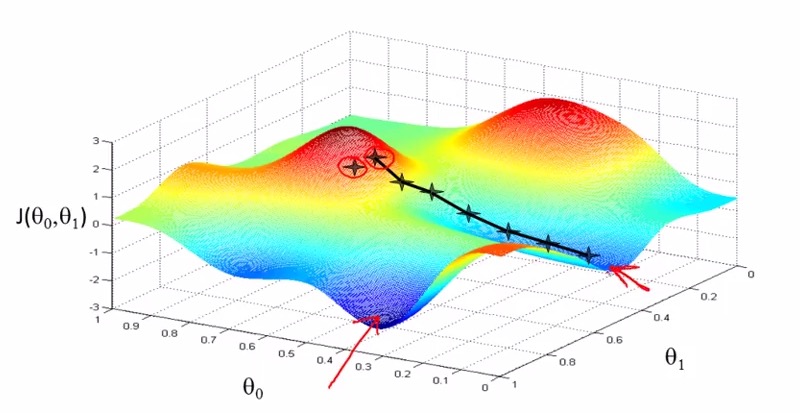
Convex function

7. Gradient descent algorithm
$ \alpha $ : learning rate

8. Gradient descent only $ \theta_{1} $
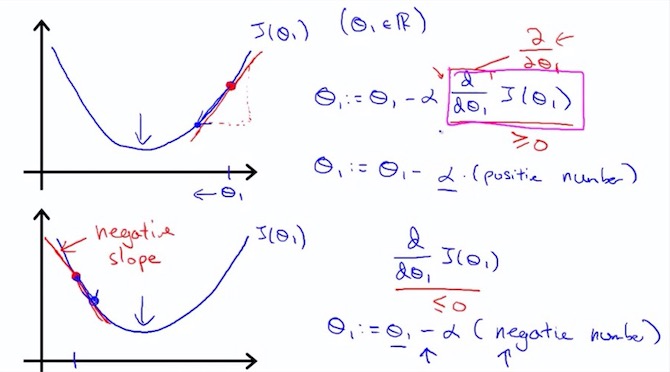
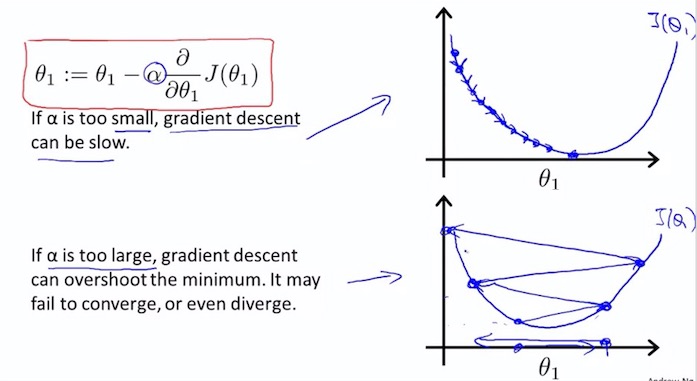
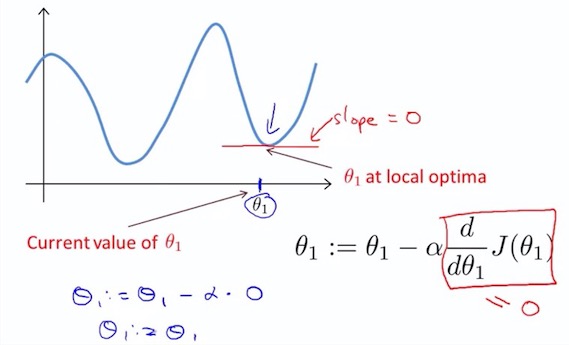
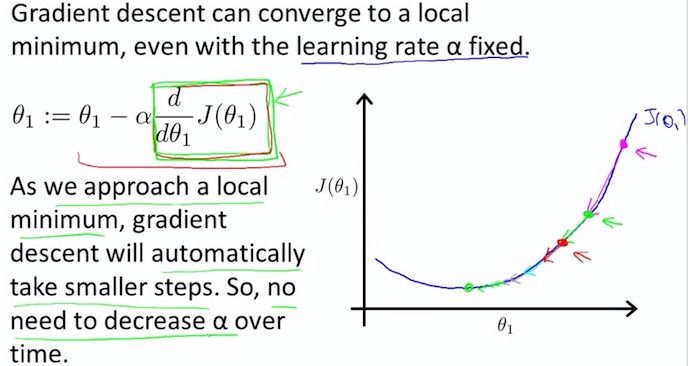
9. Linear Regression Model

9.1 Batch Gradient Descent
Batch : Each step of gradient descent uses all the training examples
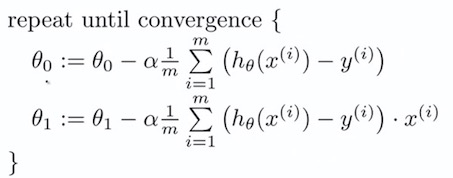
Coursera Learning Notes






Checking if Disqus is accessible...